Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

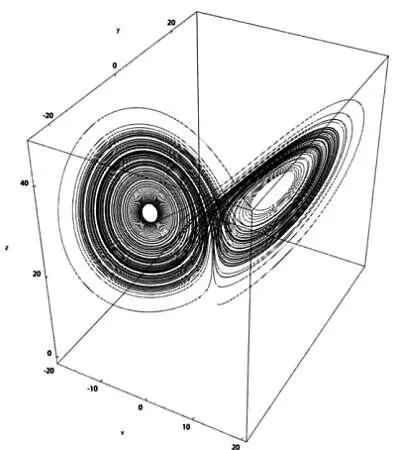
Аттрактор Лоренца — элементарная модель климата.

Любопытно, что известный эффект бабочки описал сам Лоренц в 1972 году. Его исходная формулировка звучала так: «Может ли взмах крыльев бабочки в Бразилии вызвать торнадо в Техасе?». На практике это означает, что даже малейшие изменения начальных условий, исчисляемые несколькими знаками после запятой, оказывают огромное влияние на погоду. Если сегодня в определенном месте наблюдается погода, которой соответствует точка ( х, у, z ) на правом «крыле бабочки», то погода в ближайшие дни будет описываться траекторией, берущей начало в точке ( х, у, z ).

Погода будет более или менее схожа с сегодняшней, если эта траектория будет принадлежать правому «крылу бабочки». Однако может случиться, что она достигнет левого «крыла бабочки», и прогноз существенно изменится.

Это изменение зависит от метеорологических параметров атмосферы «на сегодня», то есть от начальных условий модели: траектория, описывающая погоду в последующие дни, будет иметь тот или иной вид в зависимости от начальных условий в точке ( х, у, z ). И если погода представляет собой хаотическую систему, ее прогноз является прогнозом «индивидуальной траектории» в аттракторе климата. На практике погоду, то есть «индивидуальную траекторию», можно спрогнозировать на основе начальных условий, то есть погоды на сегодняшний день. В решении этой задачи метеорологам помогают мощные компьютеры, в которых используются климатические модели с намного большим числом переменных, чем три.

Кроме того, прогнозирование усложняется еще и потому, что климат в разных частях Земли описывается различными сценариями. В средних широтах и в тропиках погода существенно отличается. В средних широтах любое изменение погоды вызывается атмосферными явлениями, в то время как погода в тропиках определяется взаимодействием атмосферы и океана, известным как Эль-Ниньо. Самые известные его проявления — это ураганы и муссоны. Более того, некоторые явления, наблюдаемые в Тихом океане, вносят элемент неопределенности в начальное состояние атмосферы, на основе которого составляется прогноз погоды.

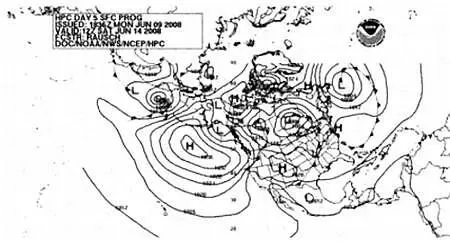
Карта с прогнозом атмосферного давления на пять дней вперед.

В 1963 году благодаря Лоренцу стало известно, насколько сложно составление точных прогнозов ввиду хаотической природы климата. Поэтому ученые решили использовать различные математические модели или начальные условия и значения параметров и составлять на их основе различные прогнозы. Существуют методы, которые позволяют оценить согласованность или степень совпадения различных прогнозов и получить средний прогноз. В этой методике также учитывается, сколько раз прогноз погоды оказывался верным для каждой модели из множества используемых. Этот подход, в котором вместо единственной модели, как во времена фон Неймана и ENIAC, используется множество моделей климата, называется мультимодельным (англ, multi-model ensemble ).

* * *

ДЖЕЙМС ЛАВЛОК И ГИПОТЕЗА ГЕИ

Джеймс Лавлок — английский исследователь (род. в 1919 году), известный как автор гипотезы Геи. Согласно Лавлоку, живые организмы отвечают за поддержание земной атмосферы. Суша, океаны, живые существа и атмосфера в совокупности образуют кибернетическую систему. Идею о кибернетической системе развила американский исследователь Линн Маргулис. Она предположила, что планета Земля в действительности представляет собой суперорганизм, способный регулировать условия, благодаря которым возможны эволюция и поддержание жизни.

Идеи Джеймса Лавлока и Линн Маргулис разделяют не все. Несогласие с ними с самого начала выразили эволюционные биологи Стивен Джей Гулд и Ричард Докинз. Дарвинисты выдвинули вопрос: быть может, именно окружающая среда отбирает живых организмов в соответствии с дарвиновской теорией эволюции путем естественного отбора? И если это так, то как объяснить, что живые организмы медленно видоизменяют окружающую среду, в которой обитают, делая ее более благоприятной для себя? Несмотря на эти возражения, существуют примеры, подтверждающие гипотезу Геи. Так, бактерии и водоросли поддерживают температуру земной поверхности, регулируют соленость морей и участвуют в накоплении углерода в осадочных горных породах. Согласно этой экологической гипотезе, вмешательство бактерий и водорослей в окружающую среду в кибернетике описывается циклами обратной связи. В качестве примера подобного механизма можно привести систему кондиционирования воздуха в комнате: повышение или понижение температуры в комнате выявляется термостатом, после чего система кондиционирования соответственно нагревает или охлаждает воздух.