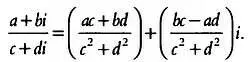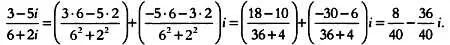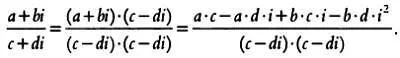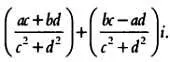Графическое представление комплексных чисел очень просто. Если предположить, что комплексное число — это точка z , то в декартовой системе координат, которую далее мы будем называть комплексной плоскостью, на горизонтальной оси X будет откладываться его вещественная часть а , на вертикальной оси Y — мнимая часть Ь .
Если мы также обозначим через r расстояние от начала координат до точки z , нетрудно показать, что это расстояние (оно называется модулем комплексного числа и обозначается | z |) равно √( a 2+ Ь 2). Более того, если учесть, что вещественная часть а равна косинусу угла α между осью х и радиус-вектором точки z , умноженному на модуль комплексного числа, а мнимая часть Ь — синусу угла α , умноженному на модуль комплексного числа, то в так называемых полярных координатах число z будет записываться следующим образом:
z = r ·(cos( α ) + i ·sin( α )).
Одно из самых любопытных свойств комплексных чисел заключается в том, что они расширяют возможности моделирования реальности, так как на них не распространяются ограничения, свойственные вещественным числам. Чтобы совершать с ними действия, можно представить, что, находясь на комплексной плоскости, ученый одной ногой стоит в вещественном мире (ему соответствует часть а ), другой — в мнимом мире (ему соответствует часть b ). При необходимости он беспрепятственно путешествует из одного мира в другой. Таким образом, к примеру, операции сложения и умножения комплексных чисел расширяют значение этих двух операций, что вы могли видеть при изучении фракталов Мандельброта и множеств Жюлиа.
Сложение и вычитание комплексных чисел
С комплексными числами могут выполняться операции сложения и вычитания. На первый взгляд это кажется сложным, но в действительности это не так. Сумма двух комплексных чисел а + bi и с + di рассчитывается следующим образом:
( а + i ) + ( с + di ) = ( а + с ) + ( b + d ) i .
К примеру, (2 + 5 i ) + (3 — i ) = (2 + 3) + (5–1) i = 5 + 4 i .
Вычитание — операция, обратная сложению, следовательно, разность комплексных чисел a + bi и с + di рассчитывается так:
( а + i ) + ( с + di ) = ( а — с ) + ( b — d ) i .
К примеру, (1 + 3 i ) — (4 + 2 i ) = (1–4) + (3–2) i = —3 + i .
Умножение и деление комплексных чисел
Также для комплексных чисел определены умножение и деление.
Произведение двух комплексных чисел а + bi и с + di определяется так:
( а + bi )·( с + di ) = ( ас — bd ) + ( ad + bc ) i .
Обратите внимание, что результат умножения можно получить следующим, более понятным способом:
( а + bi )·( с + di ) = а · с + а · d · i + b · с · i + b · d · i 2.
Напомним, что i 2= —1. Имеем:
a · c + a · d · i + b · i · c — b · d .
Приведем подобные слагаемые:
( ас — bd ) + ( ad + bc ) i .
К примеру, (2 + 6 i )·(8 + 2 i ) = (2·8–6·2) + (2·2 + 6·8) i = 4 + 52 i .
Частное двух комплексных чисел а + bi и с + di определяется так:
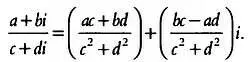
Например,
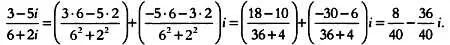
И вновь обратите внимание, что частное двух комплексных чисел — это результат выполнения следующей последовательности действий:
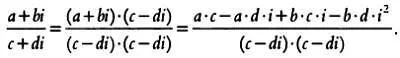
Приведем подобные слагаемые:
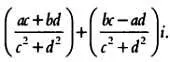
Формула Эйлера , одно из прекраснейших математических выражений
Комплексные числа полезны не только для графического изображения фракталов. Их постоянно используют инженеры при работе с электрическими цепями. Так, мощность бытовой техники выражается вещественными числами, мощность промышленных устройств — комплексными. Изучение биологических циклов, которые переживает человек, и анализ колебаний (к примеру, колебаний тела, закрепленного на пружине) в физике отчасти схожи: для решения этих задач используются комплексные числа. По этой причине те, кто знаком с комплексными числами, обычно используют формулу, которая считается одной из самых красивых и полезных в математике. Это формула Эйлера, связывающая мнимую единицу i , степень числа е и тригонометрические функции синуса и косинуса:
Читать дальше