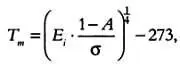Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

β( Т x ) = 1–0,003265(22,5 — T x ) 2,

β( Т y ) = 1–0,003265(22,5 — T y ) 2.

Важно заметить, что в этих выражениях учитывается локальная температура. При температуре от 5 °C до 40 °C число маргариток будет возрастать. Так как белые маргаритки отражают больше солнечного света, область, в которой они произрастают, начнет охлаждаться. Черные маргаритки, напротив, поглощают солнечный свет, и область, в которой они произрастают, будет нагреваться. В результате температуру в областях, где произрастают белые маргаритки Т х и черные маргаритки Т у , можно выразить так:

T x = Q ( A — A x ) + T m ,

T y = Q ( A — A y ) + T m

где Q — коэффициент поглощения тепла (его значение в модели равно 20), Т m — средняя температура на планете, А — альбедо планеты, А х — альбедо, вызванное белыми маргаритками, А у — альбедо, вызванное черными маргаритками.

Средняя температура на планете Т m рассчитывается согласно закону Стефана — Больцмана. Этот закон гласит, что энергия, излучаемая телом, пропорциональна температуре этого объекта, возведенной в четвертую степень. Применив этот закон, получим следующее выражение:

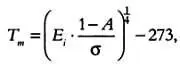
где σ = 5669·10-8 Вт/м 2·К 4— постоянная Стефана — Больцмана, Е — солнечная энергия, получаемая планетой. Обратите внимание, что если бы мы захотели смоделировать безжизненную планету, то есть планету, не населенную маргаритками, то значение альбедо было бы равным А = 0,5. Альбедо планеты А зависит от того, в какой степени поверхность планеты покрыта белыми и черными маргаритками. Это означает, что альбедо планеты А определяется следующим выражением:

А = А s · S + A x · S x + А y · S y ,

где A s — альбедо той части суши, где не растут маргаритки (площадь этой части суши равна S ), А х — альбедо, вызванное белыми маргаритками (площадь суши, где растут белые маргаритки, равна S x ), А y — альбедо, вызванное черными маргаритками (доля земной поверхности, где они произрастают, равна S y ). Обратите внимание, что выражение, по которому рассчитывается альбедо, описывает модель энергетического баланса планеты. Напомним, что черные маргаритки отражают меньше света, чем открытая суша, а белые маргаритки — больше, чем суша. Иными словами, выполняется следующее неравенство: А y < А s < А х .

Цель простейшего эксперимента с моделью «Маргариткового мира» — изучить, как изменяется доля поверхности планеты, где произрастают белые и черные маргаритки. Как правило, в модели используются следующие значения: А y = 0,25, А s = 0,50, А х = 0,75, γ = 0,30. Планета, где в изобилии растут белые маргаритки, будет холоднее, чем планета, изобилующая черными цветами. После увеличения числа белых маргариток, вызванного нагреванием планеты, температура будет снижаться, и напротив, любое снижение температуры на планете будет компенсироваться ростом числа черных маргариток. Кроме того, для некоторых значений параметров возможны два равновесных состояния: планета будет либо совершенно безжизненной, либо полностью покрытой маргаритками.

На страницах этой книги мы совершили увлекательную экскурсию, во время которой показали, что причиной удивительного прогресса биологии и биомедицины во многом стало плодотворное сотрудничество математики и науки о жизни. Использование дифференциальных уравнений, теории хаоса, программ символьных вычислений, операций над векторами и матрицами (и линейной алгебры) позволяет биоматематикам описать красоту и сложность жизни с помощью математических выражений. Благодаря математике ученые могут создавать модели, делать прогнозы относительно самых разных проявлений жизни, будь то гены, белки, клетки, организмы, популяции или экосистемы. Мы надеемся, что после прочтения этой книги читатель захочет подробнее узнать о математической биологии, или биоматематике — науке с богатыми традициями и большими перспективами.

По какой-то странной причине комплексные числа тесно связаны со многими физическими явлениями. Они присутствуют в электромагнетизме, используются в электронике, электротехнике, квантовой механике и при изучении волн. В математической биологии комплексные числа применяются при изучении биологических ритмов, занимают важное место в теории хаоса, без них невозможно представить фракталы на компьютере.