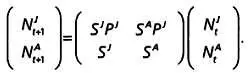Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

Передача энергии между живыми организмами, населяющими экосистему, происходит в результате питания. Так как одни организмы питаются другими, образуется пищевая цепочка, которая обычно выглядит так: растение —> травоядные —» хищники —> детритофаги . В математической модели каждое звено пищевой цепи характеризуется численностью организмов, описывается циркуляция энергии и другие аспекты. Как правило, экосистемы достаточно сложны ввиду большого числа населяющих их видов и множества связей между ними, поэтому экологи стремятся упростить модели. К примеру, экосистемы грибы и бактерии могут быть объединены в рамках единой подсистемы детритофагов. Кроме того, модель экосистемы объединяется с другими моделями и становится частью итоговой общей модели. Одной из составляющих итоговой модели является окружающая среда, будь то суша, океан и т. д. Ну а для построения моделей широко используется компьютерное моделирование.

Подобным подходом к экологии мы во многом обязаны Говарду Одуму, который в 1950-е годы впервые применил для описания экосистем схемы, напоминающие схемы электрических цепей, которые сегодня лежат в основе компьютерного моделирования. Также важным вкладом Одума в науку стало объединение экологии и теории систем.

Первые математические экологические модели описывали динамику популяций. Авторы этих моделей стремились описать изменение численности популяции и ее возрастное распределение в результате взаимодействия с окружающей средой. Эти исследования берут начало в XVIII веке, когда Томас Мальтус составил модель экспоненциального роста населения, а позднее, в 1938 году, Пьер Франсуа Ферхюльст представил логистическую модель роста.

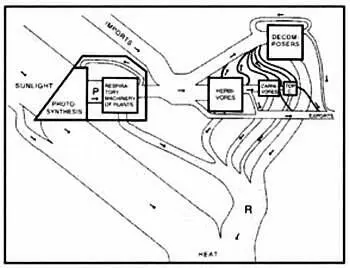
Модель, созданная на основе схем Говарда Одума. Его инновационная методология легла в основу нового способа изучения экосистем.

В 1920-е годы Вито Вольтерра и Альфред Джеймс Лотка описали две модели, которые стали настоящими столпами математической экологии. Это были модель межвидовой конкуренции и модель «хищник — жертва». Обе имели похожую структуру, однако в первой предполагалось, что рост популяций описывается логистическим уравнением, а во второй рассматривался экспоненциальный рост. Примерно двадцать лет спустя, в 1940-е годы, Патрик Лесли представил матрицу Лесли — модель структуры популяции, в которой он объединил динамику роста популяции и демографию.

В то время как в основе моделей Мальтуса, Ферхюльста и Лотки — Вольтерры лежали дифференциальные уравнения, заслуга Лесли состояла в том, что он показал применимость математических моделей, использующих матрицы.

Матричная алгебра оказалась достойным инструментом экологического и компьютерного моделирования. Матричные модели получили название BIDE (от английского Births, Immigrants, Deaths, Emigrants — «рождение, иммиграция, смерть, эмиграция»). Очевидное преимущество операций с матрицами заключалось в том, что их могли выполнять компьютеры.

В модели BIDE популяция в общем виде описывается следующим выражением:

N t+1 = N t + B + I — D — E .

* * *

ЭЛЕМЕНТАРНАЯ МОДЕЛЬ BIDE

Опишем одну из простейших экологических моделей. Допустим, что мы хотим изучить популяцию оленей, для которой известна численность самок N Jне достигших репродуктивного возраста, и число выживших самок в этой группе S Jна временном интервале от tдо t+ 1, а также численность взрослых самок N A и число выживших самок в этой группе S Aза этот же промежуток времени. Если обозначить через Р Jчисло выживших молодых самок в пересчете на каждую самку репродуктивного возраста, то численность популяции будет изменяться по следующей модели:

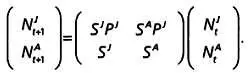
На основе этого класса элементарных моделей можно составить более сложные, к примеру модель с матрицей Лесли.

* * *

Численность популяции в момент времени t + 1 в будущем определяется ее численностью в настоящий момент времени t и совокупностью всех факторов, которые ведут к ее росту или сокращению: В — число родившихся в период времени с t по t + 1, t — число иммигрантов, присоединившихся к популяции в период времени с t по t + 1, D — число умерших в период с t по t + 1 и Е — число эмигрантов, покинувших популяцию в период с t по t + 1.