Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

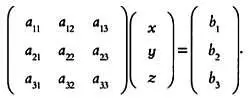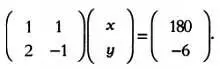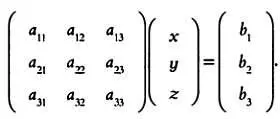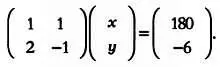
Модель памяти Хопфилдаиз восьми нейронов. Каждый нейрон в этой модели связан со всеми остальными.

* * *

Обратные матрицы применяются также для решения систем уравнений. Рассмотрим систему из трех уравнений с тремя неизвестными:

а 11х + а 12y + а 13z = b 1

а 21х + а 22y + а 23z = b 2

а 31х + а 32y + а 33z = b 3

Матрицы также используются для представления систем уравнений:

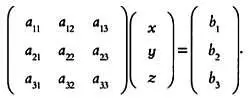
Это равенство равносильно следующему:

А · X = В .

Если мы найдем матрицу, обратную А , то есть А -1 , а затем умножим обе части равенства на эту обратную матрицу:

А -1 ·А·Х = А -1 · В ,

то, поскольку произведение А · А -1 равно единичной матрице Е , имеем:

Е · Х = А -1 · В .

Кроме того, так как произведение любой матрицы на единичную матрицу Е равно исходной матрице, получим:

Х = А - 1· В .

Таким образом, решить систему уравнений, то есть определить значения х, у, z , можно с помощью обратной матрицы коэффициентов: нужно умножить ее на вектор-столбец свободных членов системы уравнений.

Продемонстрируем этот метод на примере под названием «эксперимент энтомолога». Допустим, что мы отправились в поле в поисках определенного вида насекомых и разместили ловушки там, где эти насекомые водятся. Спустя несколько дней мы вернулись к ловушкам, чтобы собрать насекомых. В лаборатории мы установили, что в ловушках оказалось 180 насекомых. Мы разделили их на молодых (обозначим их через х) и взрослых ( у ) особей. Имеем первое уравнение системы:

х + у = 180.

На основе результатов аналогичных экспериментов, проведенных ранее, мы знаем, что для насекомых этого вида соотношение молодых и взрослых особей равно 2 к 1. Кроме того, в силу естественных причин 6 взрослых насекомых умерло:

2 х = у — 6.

Чтобы определить численность молодых и взрослых особей, нужно решить следующую систему уравнений:

х + у = 180,

2 х = у — 6.

Второе уравнение можно записать в виде: 2 х — у = —6. Система примет вид:

х + у = 180,

2 х — у = -6.

В матричной нотации эта система уравнений записывается так:

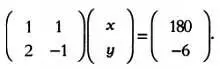
Имеет ли система уравнений решение?

Проницательные математики имеют одну достойную привычку — они не тратят время на бесполезные действия. Одним из наиболее ярких примеров этому является решение систем уравнений. Рассмотрим все возможные группы систем уравнений.

Во-первых, система может не иметь решений — в этом случае она называется несовместной. Представим, что система состоит из двух уравнений, описывающих две параллельные прямые. Поскольку прямые не пересекаются, система не будет иметь решений. Во-вторых, система может иметь бесконечно много решений, то есть быть неопределенной. Продолжив аналогию с прямыми, такая система состоит из двух уравнений, описывающих две совпадающие прямые, имеющие бесконечно много общих точек. Наконец, если система из двух уравнений описывает прямые, пересекающиеся в одной точке, она называется совместной и определенной. Ее решением будет единственная точка пересечения прямых ( х, у ).

Рассмотрим систему из трех уравнений, которая в матричном виде выглядит так:

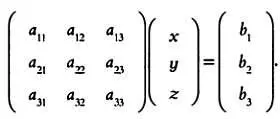
Система является совместной и определенной, если определитель матрицы А

отличен от нуля. Если определитель А равен 0, система будет либо совместной и неопределенной, либо несовместной. К примеру, система уравнений в эксперименте энтомолога в матричном виде будет записываться так:

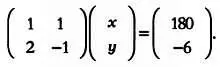
Поскольку эта система является совместной и определенной, ее можно решить.