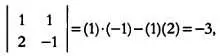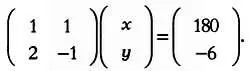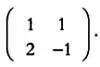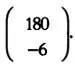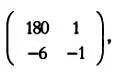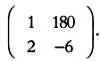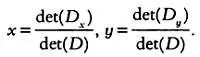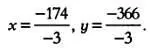Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

И действительно, если мы вычислим определитель

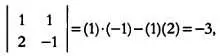
он будет отличен от нуля.

Сколько молодых и взрослых насекомых поймал энтомолог. ПравилоКрамера

Правило Крамера — это метод решения систем линейных уравнений с помощью определителей. Он был представлен Габриэлем Крамером в 1750 году.

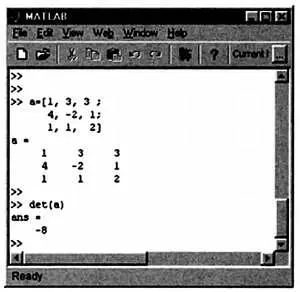
Промежуточный этап решения системы уравнений по правилу Крамерав программе MathLab.

Значения неизвестных определяются путем вычисления определителя для двух типов матриц, D j и D . Правило Крамера можно использовать только тогда, когда число уравнений равно числу неизвестных, а определитель матрицы коэффициентов отличен от нуля ( det( D) не = 0). Объясним правило Крамера на примере эксперимента энтомолога. Система линейных уравнений выглядит так:

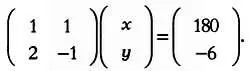
Обозначим через D матрицу коэффициентов системы:

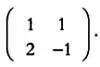
Определитель этой матрицы det( D ) равен —3. Так как система имеет две неизвестные, х и у , имеем две матрицы D j: D x и D y . Чтобы составить матрицу D j , нужно заменить j -й столбец матрицы D на вектор-столбец, образованный свободными членами системы:

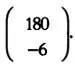
В нашем эксперименте первой неизвестной является х , поэтому j будет равен 1. Если мы заменим первый столбец матрицы D на вектор-столбец, образованный свободными членами системы, матрица D x примет вид:

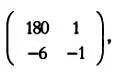
det( D x ) будет равен —174, так как (180)·(—1) — 1·(—6) = —174. Рассуждая аналогичным образом и учитывая, что второй неизвестной является у , то есть j = 2, получим, что матрица D y имеет вид:

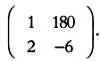
Ее определитель равен —366, так как det( D y ) равен 1·(—6) — 180·2.

Правило Крамера гласит, что решение системы уравнений можно найти, вычислив следующие выражения:

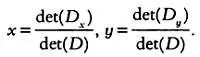
Следовательно, в эксперименте энтомолога получим:

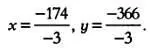
Энтомолог поймал 38 молодых особей ( х ) и 122 взрослых ( у ).

Живые существа, будь то растения, животные или микроорганизмы, взаимодействуют между собой и с окружающей средой. Биологические организмы, принадлежащие к различным видам, образуют общую природную среду — экосистему. В экосистеме можно выделить некоторые физические факторы, также называемые абиотическими, поскольку они не имеют биологической природы, и биотические факторы, которые относятся к живым обитателям экосистемы. Абиотические факторы — это все факторы, связанные с геологией и климатом: свет, вода, температура, атмосфера и состав почвы. К биотическим факторам относятся растения, травоядные и хищные животные, грибы, бактерии и т. д.

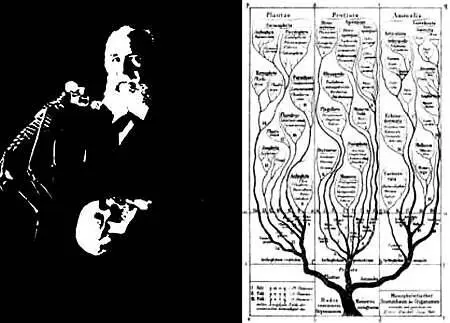
Эрнст Генрих Геккель(1834–1919) первым ввел термин «экология». Справа изображено созданное им «древо жизни».

Экосистемы изучает экология, появившаяся в XIX веке как подраздел биологии. Она преимущественно рассматривает задачи, связанные с многообразием живых существ (биологическим разнообразием), взаимосвязи между живыми организмами и окружающей средой. С момента появления экологии в ней использовались инструменты математической биологии для построения моделей, позволяющих описывать и прогнозировать экологические явления. Это привело к быстрому развитию новой науки и появлению в ней многих понятий и теорий, имеющих математическую основу.