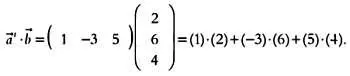Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

Достаточно помнить, что во всех подобных примерах, если вы хотите найти результат как вектор-столбец, к примеру F ->, V -> :

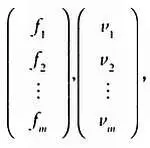
нужно сложить векторы по тому же правилу, что и матрицы, то есть F U -> + F И ->, F L -> + F M -> и V A -> + V M -> соответственно.

Помимо сложения, существует множество способов применения других операций над векторами. Так, умножение векторов успешно используется в математических моделях, описывающих наиболее характерные функции мозга.

Когда мы говорили об операциях над матрицами, мы представили модель нейронной сети, основанную на произведении вектора и матрицы:

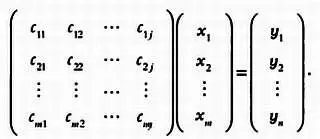
Нейронную сеть также можно представить в более простом виде:

M · u -> = v -> .

В соответствии с вышесказанным, u -> — вектор, представляющий слой входных, или афферентных, нейронов, вектор v -> — слой выходных, или эфферентных нейронов.

М — матрица связей между нейронами этих двух слоев, также известная как матрица памяти. Это название указывает на то, что именно в связях между нейронами, синапсах, мозг хранит всю известную нам информацию.

Эту гипотезу выдвинул испанский исследователь Сантьяго Рамон-и-Кахаль, а позднее развил американский ученый Дональд Хебб. В настоящее время нейробиологи считают, что именно в связях между нейронами фиксируются черты лиц знакомых нам людей, очертания букв, чисел и многие другие образы.

Сантьяго Рамон-и-Кахаль(1852–1934) в лаборатории. Справа изображен один из его рисунков, описывающих нейронные сети.

Следовательно, если мы рассмотрим произвольную строку матрицы М как вектор-строку, описывающий связи между определенным выходным нейроном и всеми входными нейронами, то состояние этого выходного нейрона можно будет вычислить так, как мы объясняли в прошлой главе. Операция над векторами называется скалярным произведением. Рассмотрим два вектора: вектор-строку а -> (исключительно из формальных соображений дополним это обозначение буквой t , что означает «транспонированный») и вектор-столбец Ь -> . Скалярное произведение этих двух векторов будет равно:

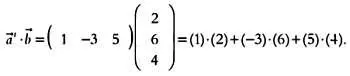
Выполнив указанные арифметические действия, получим итоговый результат, равный 4. Скалярное произведение, которое также называют внутренним произведением векторов, — это число, указывающее длину проекции вектора-строки а -> на вектор Ь -> . Если известны длины обоих векторов, | а -> | и | Ь -> |, а также угол α между ними, то скалярное произведение векторов а -> · Ь -> будет равно | а -> |·| Ь -> |·cos α . Этот результат представляет для нас особый интерес, если учесть, что | а -> |·cos α — это значение проекции вектора а -> на вектор Ь -> .

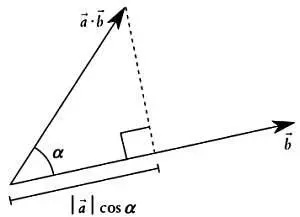
Скалярное произведение векторов а -> · Ь ->

* * *

ЧЕМУ РАВНА РАБОТА, КОГДА МЫ ТЯНЕМ ИЛИ ТОЛКАЕМ ГРУЗ?

Вычисление работы, которую мы совершаем, когда тянем груз по земле, — еще один пример, когда используется скалярное произведение векторов. Согласно законам классической механики, работа определяется как скалярное произведение действующей на предмет силы F ->и перемещения D ->. Иными словами, если векторы F ->и D ->расположены под углом друг к другу, работа Абудет равна | F|·| D|·cos α. Обратите внимание, что при неизменной силе F ->работа будет изменяться в зависимости от угла между векторами. В самом деле, если векторы F ->и D ->имеют одинаковое направление, угол между ними равен 0, и работа будет максимальной, так как косинус 0 равен 1. Нетрудно видеть, что при α> 0° работа будет меньше максимума.

* * *

Обучение. Пример с распознаванием звуков