Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

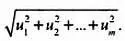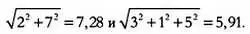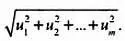
В математике модуль вектора обозначается | u |. К примеру, модули двух описанных выше векторов равны:

* * *

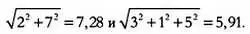
ВЕКТОРНОЕ ПРОСТРАНСТВО

В результате изучения матриц и систем линейных уравнений в XVII веке было определено понятие векторного пространства. Не будем останавливаться на нем подробнее, отметим лишь, что с точки зрения математики возможность сложения векторов (то есть выполнения операции u ->+ v ->) и умножения произвольного числа kна вектор u ->( k· u ->) вкупе с соблюдением некоторых свойств позволяет определить векторное пространство как множество векторов, обладающее определенными характеристиками. Векторное пространство является одним из основных понятий в математической биологии. Оно используется в изучении филогенеза, при классификации цепочек ДНК, в экологических моделях, при исследовании метаболизма или восприятия цветов, а также в других областях.

* * *

Если возникает необходимость определить вектор-строку, достаточно применить операцию транспонирования:

( u 1u 2 … u m ).

Далее вы узнаете, как векторы используются в изучении локомоции (перемещения животных) и при анализе нейронных сетей.

Один из самых интересных способов применения векторов — изучение локомоции животных. Кузнечики прыгают, люди могут поднимать тяжести руками, рыбы плавают, птицы летают. Понять механику этих движений помогают операции с векторами.

Если мы рассмотрим движение руки человека, один вектор можно будет сопоставить бицепсу (этот вектор будет обозначать силу сокращения мышц), второй вектор будет обозначать противодействующую силу, третий вектор — указывать вес объекта, который поднимает рука.

Сложение векторов также помогает понять функцию некоторых мускулов. Один из методов сложения векторов — это известное правило параллелограмма. Заключается оно в том, что нужно привести два вектора, сумму которых мы хотим найти, к общему началу. Затем на этих двух векторах нужно построить параллелограмм.

К примеру, если рассмотреть ногу человека и обозначить боковую часть четырехглавой мышцы бедра вектором F L -> , а среднюю часть этой мышцы — вектором F M -> , сумму этих векторов можно найти по правилу параллелограмма. Иными словами, сумма векторов F L -> + F M -> будет обозначать суммарную силу четырехглавой мышцы F -> .

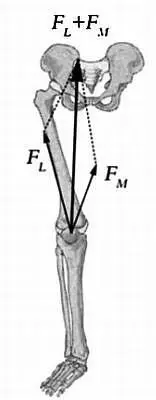
Сумма векторов, соответствующих мышцам ноги, найденная по правилу параллелограмма.

Другой классический пример — сила F -> , с которой сокращаются мышцы-сгибатели предплечья. Если представить эту силу в виде вектора, то она будет равна сумме двух других векторов, соответствующих другим мышцам. Один из этих векторов, F U -> , перпендикулярен предплечью, второй вектор, F И -> , параллелен предплечью.

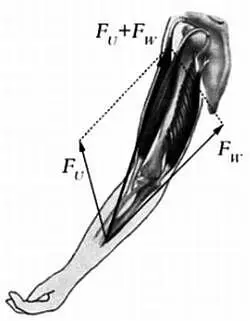
Сумма векторов, соответствующих мышцам руки, найденная по правилу параллелограмма.

Если векторов больше двух, их сумму можно найти по правилу многоугольника. Заключается оно в том, что конец каждого вектора совмещается с началом следующего. Суммой исходных векторов будет вектор, начало которого совпадает с началом первого вектора, конец — с концом последнего вектора. Этот метод полезен при вычислении скорости движения корабля, полета птиц, перемещения пловца или рыбы.

В примерах с птицей или рыбой результирующая скорость будет равна сумме всего двух векторов. Но в силу особенностей задачи для сложения векторов используется не правило параллелограмма, а правило многоугольника.

Допустим, что рыба или птица движется в воде или в воздухе со скоростью, обозначаемой вектором V A ->, V M -> — скорость течения воды (или ветра). Как следствие, вектор результирующей скорости V -> будет равен сумме векторов V A -> и V M -> , определяемой по правилу многоугольника.

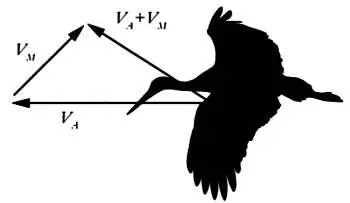
Сумма векторов в примере с полетом птицы, найденная по правилу многоугольника.