Josep Carrera - Трехмерный мир. Евклид. Геометрия

РИС. 2

Несмотря на определения 2, 3 и 4 из книги I, Евклид ни разу не объяснил, что такое прямая, каковы ее свойства и каким критериям она должна отвечать. Тем не менее он ясно определил, что прямые конечны и их концами являются точки. В действительности Евклид занимался отрезками прямых. Но когда он говорит о равной длине диаметра в определении круга, то использует понятие расстояния. Для прямых его применил позже Архимед в первой аксиоме своего сочинения «О шаре и цилиндре»: «Прямая — кратчайшее расстояние между двумя точками». Как мы увидели на примере предложения 4, Евклид использовал постулаты, не устанавливая их. В доказательстве предложения 1 книги I, проанализированном в главе 2, содержится утверждение, которое мы сейчас подробно рассмотрим:

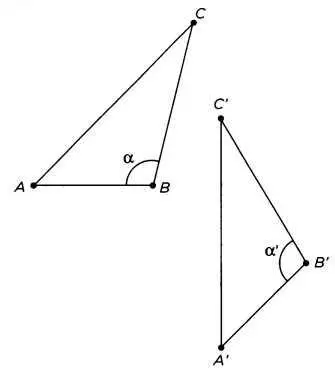
Проведем прямые СА и СВ из точки пересечения двух окружностей С.

Что может служить гарантией существования точки С по Евклиду? Ничего, кроме рисунка, иллюстрирующего доказательство. Но это неприемлемо, так как рисунок может считаться правильным, только если точка С существует (вспомним изображения невозможных треугольников, использующиеся в доказательствах методом доведения до абсурда).

Вопрос искривления возникает в «Началах» неявно. Перед тем как перейти к постулату о параллельных прямых, Евклид устанавливает очень интересный результат:

Книга I, предложение 17. Во всяком треугольнике сумма двух любых углов меньше двух прямых углов.

Чтобы правильно понять эту задачу, мы должны внимательно следовать за рассуждениями Евклида. Он хочет доказать, что сумма углов

1. Он делит сторону AG пополам и получает точку Е (Книга I, предложение 10).

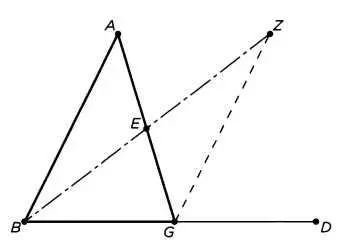
2. Соединяет В и Е (постулат 1) и удваивает этот отрезок (постулат 2 и книга I, предложение 2). Получается точка Z.

3. Соединяет ее с точкой G (постулат 1). Евклид получает два равных треугольника (книга I, предложение 4), так как стороны ZE и EG треугольника ZEG равны сторонам BE и ЕА треугольника БЕЛ соответственно, по построению, а углы <���АЕВ противоположны вершине и равны (книга I, предложение 15). Следовательно, оба треугольника равны, а угол

Евклид получил такой результат, поскольку точка Z располагается внутри угла

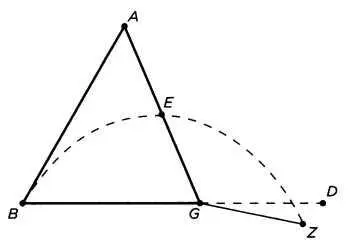
В постулате 5 Евклид утверждает, что при некоторых условиях две прямые пересекаются: «Существует точка, принадлежащая им обеим». А в случае с окружностями он принимает это за такой очевидный факт, что не считает нужным говорить об этом. Здесь мы опять сталкиваемся со скрытым постулатом.

Равносторонний треугольник, построенный на отрезке АВ в первом предложении, существует, поскольку построение Евклида верно; но оно зависит от существования точки С. В реальности, в которой этой точки нет, не будет и треугольника. От этого зависят многие из первых доказательств Евклида. Возможность построения в «Началах» зависит от возможности построения точек. Ученый определяет необходимые и достаточные условия, при которых две прямые пересекаются, и правильно обозначает точки, появляющиеся таким образом. Но при этом он не говорит, при каких условиях пересекаются прямая и окружность, и следовательно, точки, получающиеся в местах их пересечения, как бы не существуют.

Я прихожу все более к убеждению, что необходимость нашей геометрии не может быть доказана, по крайней мере человеческим рассудком и для человеческого рассудка.

Карл Фридрих Гаусс

Хотя он мог бы сделать это очень просто, достаточно было уточнить, например в случае с окружностями, следующее.

Постулат о пересечении двух окружностей.Если расстояние между центрами двух окружностей меньше половины суммы их диаметров [то есть меньше суммы радиусов этих окружностей] ,то эти окружности пересекаются в двух точках.

Аналогичным образом можно определить условие, позволяющее выявить существование двух точек, образованных в результате пересечения окружности и прямой: прямая и окружность пересекаются [в двух точках], если перпендикуляр, идущий от центра окружности к прямой, меньше ее радиуса. Но Евклид ничего не говорит по этому поводу.