Josep Carrera - Трехмерный мир. Евклид. Геометрия

Все ученые, занимающиеся «Началами», согласны в том, что их структура и, в частности, постулат 5 (мы будем кратко обозначать его П5) принадлежат самому Евклиду. Это знаменитый постулат о параллельных прямых, который в формулировке Евклида гласит, что «в определенных условиях две прямые неизбежно пересекутся». Евклид впервые применяет его только в предложении 29 первой книги. Та часть геометрии, которая не зависит от этого постулата, получила название абсолютной геометрии. Дословно в пятом постулате говорится следующее.

Постулат 5 (П5). Если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные эти две прямые неограниченно встретятся с той стороны, где углы, меньшие двух прямых.

Обычно постулат о параллельных прямых изучается не в этой оригинальной формулировке, а в том виде, в котором его изложил шотландский математик Джон Плейфэр (1748— 1819), профессор математики, а впоследствии и философии в Эдинбургском университете.

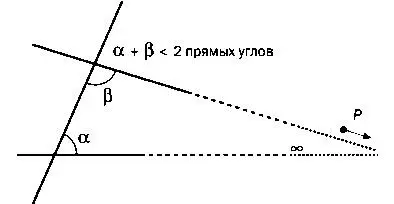
Постулат Плейфэра (ПП). В плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.

Это утверждение имеет точно такой же смысл, как и постулат Евклида, и подчеркивает, что для П5 необходимы два условия: с одной стороны, существование «прямой, параллельной данной прямой, проведенной через точку, не лежащую на последней», а с другой стороны, эта прямая должна быть единственной. Это существование Евклид дает в предложении 31:

При помощи пятого постулата Евклид предотвращает асимптотичность «искривления» прямых, как в случае с гиперболой и ее асимптотой (эта предосторожность тем более необходима, поскольку, как мы уже увидели, Евклид не дает полного определения прямой, так что мы не знаем ее полных основных свойств).

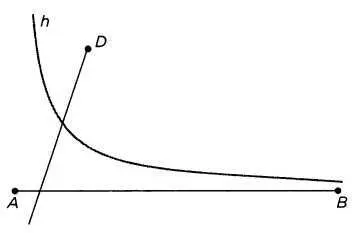
В случае с кривыми, например, то, что одна все больше приближается ко второй, не означает, что они обязательно пересекутся, как видно на рисунке: гипербола постепенно приближается к прямой — своей асимптоте,— но никогда не коснется ее.

Книга I, предложение 31. Через точку Р> не лежащую на прямой АВ Увсегда можно провести прямую линию, параллельную данной прямой.

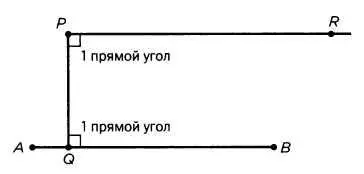
Проведем через точку Р линию PQ, перпендикулярную АВ (Q находится на прямой АВ или на ее продолжении, которое можно построить при помощи циркуля и линейки, согласно предложению 12). Таким же образом проведем через Р прямую PR, перпендикулярную PQ. Очевидно, что прямые PR и АВ параллельны, потому что в противном случае они бы пересеклись в некой точке, например R, и мы получили бы треугольник ΔQPR с двумя прямыми углами. Но это невозможно (поскольку противоречит предложению 16 книги I), следовательно, существование параллельной доказано. Теперь мы должны доказать, что эта прямая всего одна. Для этого необходимо прибегнуть к ложному (или идеальному) геометрическому объекту, который уже подразумевает правильность того, что мы хотим доказать. Получается, факт единственности такой параллельной не вытекает ни из какого другого постулата. Как мы увидим дальше, это привело к настоящему перевороту, поскольку вынуждало поставить под сомнение авторитет Евклида.

Доказать единственность параллельной можно, приняв за истину евклидову геометрию.

Через точку Р, не лежащую на прямой АВ, всегда можно провести единственную прямую, параллельную данной.

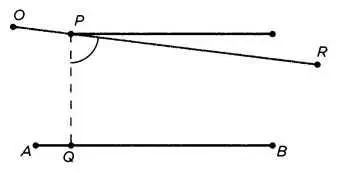
Если бы существовали две прямые, параллельные АВ (вводится дополнительная фигура, воображаемая, поскольку основана на ложной предпосылке), это были бы первая (та, которая образует прямой угол с PQ в точке Р) и PR. Следовательно, угол

Говоря о геометрии, невозможно не задаться вопросом: какова же истинная геометрия природы? Несомненно, одна из целей аксиоматизации состоит в том, чтобы уловить истину сущего. Но, возможно, на самом деле мы просто улавливаем истинность того, что представляем, то есть порождения человеческого разума, необязательно совпадающего с реальностью.