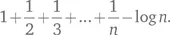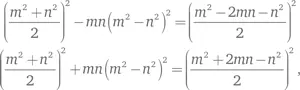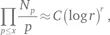Иэн Стюарт - Величайшие математические задачи

С ростом x растет и √ x , так что 1/√ x стремится к 0, а отношение стремится к 1. Но разность составляет √ x и становится все больше с ростом x . К примеру, когда x равен 1 трлн, √ x равен 1 млн.

Постоянная Эйлера — это предел при n , стремящемся к бесконечности выражения

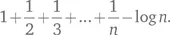
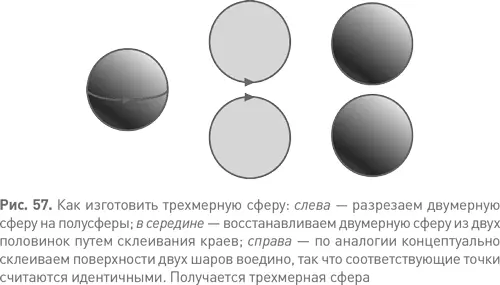
Единичная трехмерная сфера содержит все точки с координатами ( x, y, z, w ), такими, что x ² + y ² + z ² + w ² = 1. Есть несколько способов сделать трехмерную сферу более интуитивно понятной. Ее можно рассматривать по аналогии с двумерной сферой и проверять посредством координатной геометрии. Одно такое описание («заполненный шар, все точки поверхности которого тождественны между собой») дано в тексте, а на рис. 57 можно увидеть еще одно. Чтобы установить аналогию, заметим, что при разрезании двумерной сферы вдоль экватора мы получаем две полусферы. Каждая из них непрерывно преобразуется в плоский диск. Чтобы восстановить двумерную сферу, мы просто отождествляем соответствующие точки на границах этих двух дисков. В каком-то смысле мы изготовили карту двумерной сферы из двух плоских дисков, так же как картографы создают плоские проекции нашей круглой планеты. Трехмерную сферу можно построить при помощи аналогичной процедуры. Возьмем два заполненных шара и отождествим между собой соответствующие точки их поверхностей. Теперь оба они имеют одну и ту же поверхность (ведь мы их отождествили), и эта поверхность представляет собой двумерную сферу. Она образует «экватор» трехмерной сферы.

Традиционно считается, что мы говорим о сложении и используем обозначение a + b , когда коммутативный закон соблюдается, но говорим об умножении и используем обозначение ab , когда он может и не соблюдаться. Здесь, однако, я не следовал этому принципу, поскольку эта книга — не учебник по теории групп, а термин «сложение» представляется более естественным.

Начнем счет с нуля. Всякий раз, проходя остановку на пути против часовой стрелки, увеличиваем счет на 1; проходя ее против часовой стрелки, уменьшаем на 1. В конце поездки добавляем 1, если приехали против часовой стрелки, и вычитаем 1, если приехали по часовой стрелке. Окончательный результат подсчета скажет вам, сколько раз вы обогнули окружность в общем направлении против часовой стрелки.

Формула Стирлинга утверждает, что n ! приблизительно равно √(2π n )( n / e ) n .

Леонардо нашел семейство решений

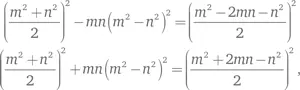
где m, n — нечетные числа. Роль d здесь выполняется числом mn ( m ² — n ²2), а x равен m ² + n ²2/2. Выбор m = 5, n = 4 ведет к тому, что mn ( m ² — n ²) = 720. Более того, 720 = 5 × 12². Разделив x на 12, получим ответ.

Если x — n, x и x + n представляют собой квадраты, то их произведение тоже квадрат и равно x ³ — n ² x . Следовательно, уравнение y ² = x ³ — n ² x имеет рациональное решение. Более того, y не равен нулю, в противном случае x = n, т. е. x и 2 x — квадраты, что невозможно, поскольку число √2 иррационально.

Напротив, если x и y удовлетворяют кубическому уравнению и y не равен 0, то a = ( x ² — n ²)/ y, b = 2 nx / y и c = ( x ² + n ²)/ y удовлетворяют уравнениям a ² + b ² = c ² и ab /2 = n .

Иными словами:

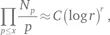
где r — ранг, C — константа, а знак ≈ означает, что отношение двух частей этого выражения стремится к 1 при x , стремящемся к бесконечности.

Наиболее вероятная причина заключается в том, что существуют естественные варианты перевода с соответствующих языков, которыми пользуются лучшие математики обеих областей.

Я не знаю, почему b — не число бананов. Возможно, потому, что в послевоенной Британии бананы были экзотикой и в продаже попадались редко.