Иэн Стюарт - Величайшие математические задачи

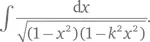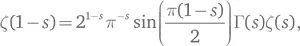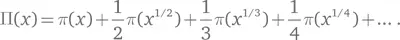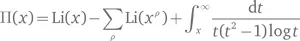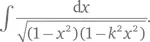
Это функция, обратная эллиптической функции, обозначаемой как sn. Такая функция существует для каждого значения k . Устроено все примерно так же, как в случае с sin и arcsin, но хитрее.

Один корень p -й степени из единицы равен комплексному числу

а остальные представляют собой его степени ζ 2, ζ 3, … ζ p− 1. Чтобы понять почему, вспомните, что тригонометрические функции синус и косинус определяются через прямоугольный треугольник (см. рис. 56 слева). Обозначив стороны треугольника традиционными a, b, c , мы определяем синус и косинус угла A как sin A = a / c , cos A = b / c .

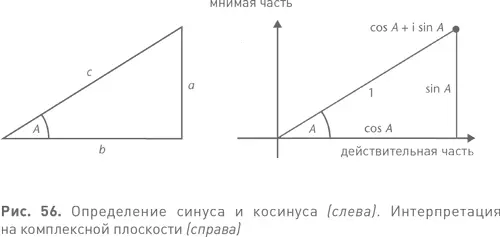
Если мы возьмем c = 1 и поместим этот треугольник на комплексную плоскость, как на рис. 56 справа, то вершина, в которой встречаются c и a , представляет собой точку

Несложно доказать, что для любых углов A и B

а это ведет непосредственно к формуле Муавра

для любого натурального n . Поэтому

для любой степени 1, где ζ, ζ 2, ζ 3, …, ζ p− 1есть корень p -й степени из единицы. На этом мы остановимся, поскольку ζ p = 1 и, соответственно, для более высоких степеней новых чисел не появится.

Введем понятие нормы.

имеющее замечательное свойство

Тогда

Любой собственный делитель любого из этих четырех чисел должен иметь норму 2 или 5 (собственные делители их норм). Но уравнения a ² − 15 b ² = 2 и a ² − 15 b ² = 5 не имеют целых решений. Следовательно, собственных делителей не существует.

А может быть, и нет. Владимир Кривченков установил, что энергия основного состояния и первых возбужденных состояний для квантовой задачи трех тел может быть рассчитана вручную. Но в классической механике аналогичная проблема оказывается менее решаемой из-за хаоса.

Более формально это называется временем Ляпунова.

Существует вариант, где 1/log t интегрируется от 2 до x , а не от 0 до x . Это помогает обойти технически сложный момент при t = 0, где log t не определен. Иногда для этого варианта используется обозначение Li( x ), а определенная в тексте функция называется Li( x ).

Это следует из занятной формулы Римана

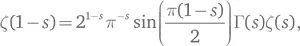
где Г ( s ) — классическая функция, известная как гамма-функция и определенная для всех комплексных s . Правая ее сторона определена, когда действительная часть s больше 1.

Риман определил еще одну похожую функцию

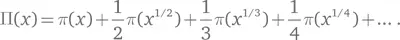
которая подсчитывает скорее простые степени, чем простые числа. Из этого можно восстановить π( x ). Затем он доказал точную формулу для этой модифицированной функции в терминах логарифмических интегралов и связанного интеграла:

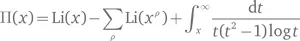
Здесь Σ — сумма по всем значениям ρ, при которых ζ (ρ) равна 0, исключая отрицательные целые числа.

К примеру, асимптотична √ x : их отношение равно