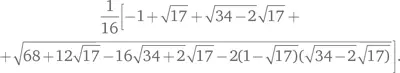Нахождение конечного разбиения квадрата и собирания из этих частей круга известно как квадратура круга Тарского. Миклош Лацкович решил эту задачу в 1990 г. Его метод неконструктивен и использует теорему выбора, при этом число частей, на которые нужно делить квадрат, огромно — около 10 50.
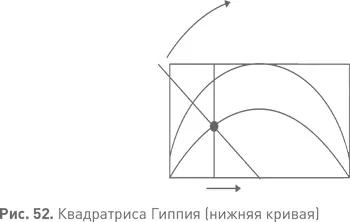
Квадратриса Гиппия — это кривая, описываемая точкой пересечения вертикальной прямой, движущейся равномерно через прямоугольник, и прямой, которая равномерно поворачивается вокруг середины нижней стороны прямоугольника (см. рис. 52). Такое соотношение превращает любой вопрос о делении угла в вопрос о соответствующем делении отрезка. К примеру, чтобы разделить угол натрое, нужно всего лишь разделить натрое соответствующий отрезок прямой. См.: http://www.geom.uiuc.edu/~huberty/math5337/groupe/quadratrix.html.
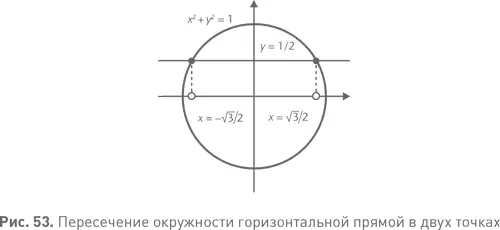
Вот красноречивый пример. Геометрически если прямая пересекается с окружностью и не является касательной, то она имеет с окружностью ровно две общие точки. Возьмем прямую, параллельную горизонтальной оси, на расстоянии 1/2 над ней (см. рис. 53). Эта прямая описывается очень простым уравнением: y = 1/2. (При любом x мы имеем одно и то же значение y .) Если y = 1/2, то уравнение x ² + y ² = 1 превращается в x ² + 1/4 = 1. Отсюда x ² = 3/4, а 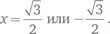 Алгебра говорит, что прямая пересекает единичную окружность ровно в двух точках
Алгебра говорит, что прямая пересекает единичную окружность ровно в двух точках 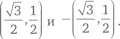 Это вполне согласуется с рис. 53 и чисто геометрическими соображениями.
Это вполне согласуется с рис. 53 и чисто геометрическими соображениями.
Строго говоря, многочлен, о котором идет речь, должен иметь целые коэффициенты и быть несокращаемым (т. е. не являться произведением двух многочленов меньших степеней с целыми коэффициентами). Степень многочлена, равная степени двойки, — необходимое, но не достаточное условие для существования построения при помощи циркуля и линейки. Если степень не равна степени двойки, построение существовать не может. Если равна, то для решения вопроса о его существовании необходим дальнейший анализ.
Обратное тоже верно: данные построения для правильных трех— и пятиугольников можно получить из построения 15-угольника. Идея в том, что 2/5 − 1/3 = 1/15. В отношении простых степеней есть один тонкий момент. Эти рассуждения не позволяют построить, скажем, девятиугольник, хотя построение для простых делителей числа (а именно треугольника) существует. Гаусс доказал, что для нечетных простых чисел, возведенных в степень больше 1, построение невозможно.
Чтобы разобраться в этом утверждении, разложим квадратный многочлен на линейные множители. Тогда x ² − 1 = ( x + 1) ( x − 1), что равно нулю, если любой из множителей равен нулю, так что x = 1 или x = −1. Те же рассуждения можно применить к x ² = xx : это равно нулю, если нулю равен один из множителей. В данном случае они совпадают, но наличие двух множителей x отличает этот случай от чего-нибудь вроде x ( x − 1), где множитель x один. При ответе на вопрос о том, сколько решений имеет алгебраическое уравнение, подобную «множественность» лучше учитывать.
При n = 9 второй множитель будет
x 8+ x 7+ x 6+ x 5+ x 4+ x 3+ x 2+ x + 1.
Но он и сам является составным: он равен
( x 2+ x + 1) ( x 6+ x 3+ 1).
Гауссова характеристика чисел, допускающих построение, требует, чтобы степень каждого несократимого множителя была степенью 2. Но степень второго множителя — 6 — не является степенью 2.
Гаусс доказал, что 17-угольник можно построить, если вы умеете строить отрезки длиной
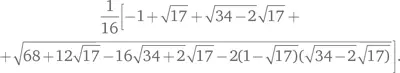
Поскольку квадратный корень всегда можно построить, это вполне эффективно решает задачу. Другие математики нашли более очевидные построения. Ульрих фон Гугенин опубликовал первое из них в 1803 г., а Г. Ричмонд в 1893 г. нашел более простое. На рис. 54 возьмем два перпендикулярных радиуса AOP 0и BOC окружности. Пусть OJ = 1/4 OB, а угол OJE = 1/4 OJP 0. Найдем F, такое, что угол EJF равен 45°. Построим окружность с диаметром FP 0; она пересекается с OB в точке K. Проведем через K окружность с центром в точке E; она пересечет AP 0в точках G и H. Построим в этих точках перпендикуляры к AP 0, назовем их HP 3и GP 5. Тогда P 0, P 3, P 5представляют собой соответственно нулевую, третью и пятую вершины правильного 17-угольника. Теперь несложно построить и остальные вершины.
Читать дальше
Конец ознакомительного отрывка
Купить книгу


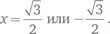 Алгебра говорит, что прямая пересекает единичную окружность ровно в двух точках
Алгебра говорит, что прямая пересекает единичную окружность ровно в двух точках 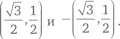 Это вполне согласуется с рис. 53 и чисто геометрическими соображениями.
Это вполне согласуется с рис. 53 и чисто геометрическими соображениями.