Иэн Стюарт - Величайшие математические задачи

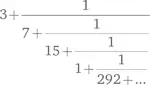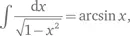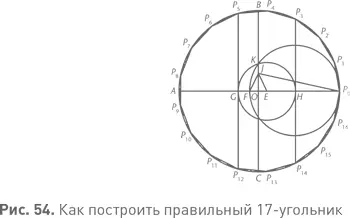
Ф. Ришло опубликовал построение правильного 257-угольника в 1832 г. Йоханн Хермес посвятил десять лет жизни исследованию 65 537-угольника. Его неопубликованную работу можно найти в Университете Геттингена, но считается, что в ней есть ошибки.

Типичная цепная дробь выглядит примерно так:

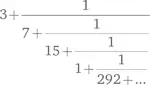
Данная конкретная цепная дробь представляет собой начало дроби, представляющей число π.

Если границы могут быть по-настоящему сложными, не как на карте, а гораздо более извилистыми, то общую «границу» могут иметь сколько угодно стран. Этот неочевидный результат иллюстрирует конструкция, известная как «озера Вады».

До недавнего времени статья в Nature считалась последней публикацией, посвященной этой проблеме, почти за 100 лет, но историк математики Робин Уилсон отыскал более позднюю статью Кейли.

При работе в двойственной сети пусть F — число граней (включая одну большую грань, окружающую сеть целиком), E — число ребер, а V — число вершин. Можно считать, что каждая грань двойственной сети имеет по крайней мере три ребра — ведь если в ней есть грань только с двумя ребрами, то она соответствует «лишней» вершине первоначальной сети, в которой встречаются всего два ребра. Такую вершину можно удалить, а два ребра объединить в одно.

Каждое ребро граничит с двумя гранями, и каждая грань имеет по крайней мере три ребра, потому E ≥ 3 F /2 или, что то же самое, 2 E /3 ≥ F . Согласно уравнению Эйлера, F + V — E = 2, так что 2 E /3 + V — E ≥ 2. Из этого следует, что 12 + 2 E ≤ 6 V .

Пусть V m — это число вершин с m соседями. Тогда V = V 6 + V 7+ V 8+ …

Поскольку каждое ребро соединяет две вершины:

Подставив в неравенство, получаем:

так что 12 + V 7+ 2 V 8+ … ≤ 0,

что невозможно.

Термин «цепочка» здесь неточен, потому что предполагает линейную последовательность. Цепочка Кемпе может содержать петли и разветвляться.

Поскольку пространство бесконечно, шариков в нем тоже бесконечно много, так что общий объем и пространства, и шариков также бесконечен. Мы не можем определить плотность как ∞/∞, потому что эта величина математически не определена. Вместо этого мы последовательно рассматриваем все более крупные области пространства и берем верхний предел отношения областей, заполненных шариками.

Хейлс использовал несколько различных определений того, что я называю клеткой. Последнее — «звезда декомпозиции». В моем описании опущены некоторые принципиально важные отличия; так общая идея получается более понятной.

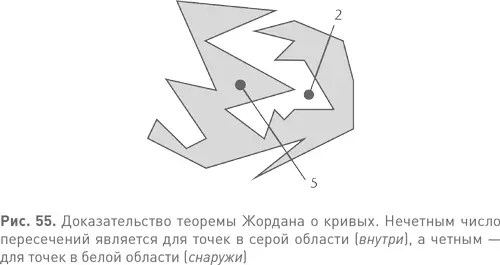
Пусть область представляет собой многоугольник, как на рис. 55. Для любой точки, не лежащей на линиях многоугольника, существует проходящая через нее прямая, которая выходит за пределы описывающей многоугольник окружности и не проходит ни через одну его вершину. (Вершин — конечное количество, а прямых — бесконечное, есть из чего выбрать.) Эта прямая пересекает многоугольник конечное число раз, причем число это либо четное, либо нечетное. Определим, что внутренняя часть состоит из точек, для которых это число нечетное, а внешняя — из точек, для которых оно четное. Без труда доказывается, что каждая из этих областей является связной, а многоугольник их разделяет (см. рис. 55).

Расширим это загадочное замечание: вот формула

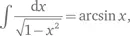
где арксинус (arcsin или sin −1) представляет собой функцию, обратную синусу. Иными словами, если y = sin x , то x = arcsin y .

К примеру, пусть k — любое комплексное число. Рассмотрим интеграл