Джордан Элленберг - Как не ошибаться. Сила математического мышления

Проще говоря, если вы находитесь в больнице, то вы попали туда по какой-то причине. Если вы не диабетик, тогда больше вероятность того, что эта причина – высокое кровяное давление. Следовательно, то, что на первый взгляд кажется причинно-следственной связью между гипертонией и диабетом, на самом деле всего лишь статистический фантом.

Этот эффект может работать и в обратном направлении. В реальной жизни наличие двух болезней с большей долей вероятности может отправить вас в больницу, чем одна болезнь. Все 120 пациентов, которые являются одновременно и гипертониками, и диабетиками, могут оказаться в больнице, но 90 % относительно здоровых людей, страдающих только одной болезнью, остаются дома. Более того, в больнице можно оказаться и по другим причинам: например, в первый снежный день года многие пытаются привести свои снегоочистители в порядок руками и в результате отрезают палец. В таком случае общая совокупность пациентов больницы может выглядеть так:

10 человек без диабета и гипертонии, но с отрезанным пальцем;

18 человек с гипертонией, но без диабета;

28 человек с диабетом, но без гипертонии;

120 человек с гипертонией и диабетом.

Теперь после проведения исследования в больнице вы обнаружите, что 120 из 148 диабетиков, или 81 %, страдают гипертонией. Однако только 18 из 28 пациентов, не страдающих диабетом, или 64 %, страдают гипертонией. Создается впечатление, что гипертония увеличивает вероятность того, что у вас есть еще и диабет. Но это снова иллюзия: мы с вами установили всего лишь тот факт, что множество людей, попадающих в больницу, не является случайной выборкой из генеральной совокупности.

Ошибка Берксона имеет смысл и за пределами медицины; на самом деле эту концепцию можно применить за пределами тех областей, в которых характеристики поддаются точной количественной оценке. Возможно, вы обратили внимание на то, что среди всех мужчин [285]в вашем списке возможных партнеров красивые мужчины, как правило, не бывают хорошими, тогда как хорошие не бывают красивыми. Может, причина в том, что симметричное лицо делает человека жестоким? Или в том, что хорошее обхождение с другими людьми делает человека некрасивым? Возможно. Но так не должно быть. Посмотрите на представленный ниже «большой квадрат мужчин».

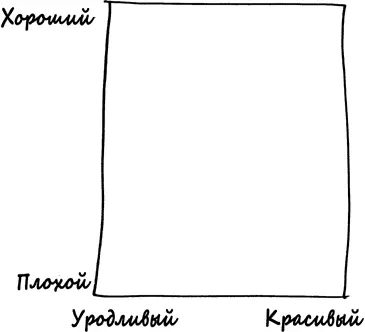
В качестве рабочей гипотезы я допускаю, что все мужчины распределены по этому квадрату равномерно; в частности, здесь примерно в равном количестве присутствуют хорошие красивые мужчины, хорошие уродливые мужчины, плохие красивые мужчины и плохие уродливые мужчины.

Однако у хорошего характера и красоты есть общее следствие: эти качества относят мужчин к той группе, на которую вы обращаете внимание. Скажите честно: ведь вы даже не станете рассматривать в качестве кандидатов в спутники жизни уродов с плохим характером. Таким образом, внутри «большого квадрата» есть «небольшой треугольник приемлемых мужчин».

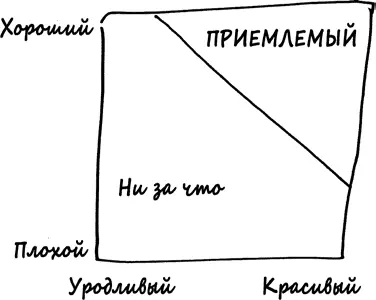
Теперь источник этого явления очевиден. Самые красивые мужчины в вашем треугольнике представляют весь диапазон личностей, от самых добрых до самых жестоких. В среднем они почти такие же хорошие, как среднестатистический мужчина во всей совокупности мужчин, которая, надо признать, не такая уж хорошая. Точно так же самые хорошие мужчины всего лишь в среднем красивы. Однако некрасивые парни, которые вам нравятся (они образуют крошечный сегмент треугольника), очень хорошие люди – они должны быть такими, иначе вы их вообще не заметите. Отрицательная корреляция между внешностью и личностью в вашем списке потенциальных партнеров абсолютно реальна. Однако, если вы попытаетесь улучшить телосложение своего парня, научив его вести себя плохо, вы станете жертвой ошибки Берксона.

По такому же принципу действует литературный снобизм. Вы знаете, почему популярные романы настолько ужасны? Причина не в том, что массовый читатель не ценит качество. Причина в том, что существует «большой квадрат романов», а также в том, что вы слышали только о тех романах, попадающих в «треугольник приемлемых романов», которые являются либо популярными, либо хорошими. Если вы заставите себя прочитать непопулярные романы, выбранные, по сути, случайным образом (я входил как-то в жюри по присуждению литературных премий, так что я реально занимался этим), вы обнаружите, что большинство из них, как и популярные романы, довольно низкого качества.