Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

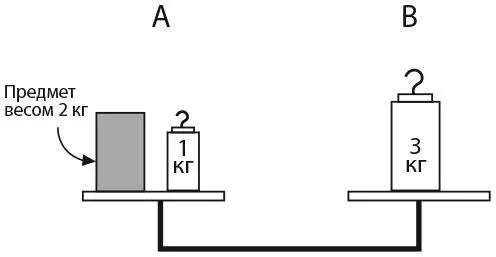
Не существует других способов уравновесить 2 килограмма с помощью двух разных гирь, поэтому мы используем две гири весом 1 и 3 килограмма.

С помощью гирь на 1 и 3 килограмма мы можем взвесить предметы весом до 4 килограммов. Какая самая большая гиря позволит взвесить 5-килограммовый предмет на чаше А с использованием обеих чаш?

Если повторить описанную выше процедуру и разместить предмет весом 5 килограммов на чаше А со всеми гирями из нашего набора, то есть 1 + 3 = 4 килограмма, то для уравновешивания на чашу Б нам понадобится положить 9-килограммовую гирю.

Теперь мы располагаем гирями 1, 3 и 9 килограммов. С их помощью можно взвесить предметы весом до 13 килограммов. Какая самая большая гиря позволит нам взвесить 14-килограммовый предмет на чаше А, используя обе чаши?

Согласно представленной выше логической схеме, это будет гиря весом 14 + 13 = 27 килограммов.

Теперь наш комплект гирь: 1, 3, 9 и 27 килограммов. Так что далее можем взвесить предметы весом до 40 килограммов. Использование обеих чаш весов позволило нам сократить количество гирь в наборе с шести до четырех.

Возможно, вы заметили закономерность: если гири располагать на одной чаше весов, числа образуют последовательность, каждый очередной член которой в два раза больше предыдущего. Если гири можно класть на обе чаши, то каждый очередной член последовательности будет втрое больше предыдущего. Подобно тому как последовательность удваивающихся чисел соотносится с двоичной системой счисления, последовательность утраивающихся чисел соотносится с троичной системой счисления, то есть с троичными числами, в которых используются только 0, 1 и 2.

Например, число 1020 в троичной системе означает, что в разряде единиц ничего нет, в разряде тройки – 2, в разряде девяток ничего нет, а в разряде двадцати семи находится 1. Следовательно, 6 + 27 = 33, то есть число 1020 в троичной системе соответствует числу 33 в десятичной системе.

К тексту

Давайте пронумеруем монеты от 1 до 12.

Во время первого взвешивания нам нужно сравнить вес монет 1, 2, 3, 4 и 5, 6, 7, 8. Если чаши весов уравновешены, значит, фальшивая монета находится среди оставшихся – 9, 10, 11 и 12.

Возьмем три из этих монет и сравним их вес с любыми тремя уже взвешенными монетами, среди которых, как нам известно, фальшивых нет. Предположим, это монеты 1, 2, 3 и 9, 10, 11.

Если чаши весов находятся в равновесии, значит, фальшивая монета – 12. А чтобы определить, легче или тяжелее она остальных, во время третьего, последнего взвешивания необходимо сравнить ее вес с весом любой другой монеты.

В случае если чаши весов не уравновешены, фальшивой монетой будет 9, 10 или 11. А легче она или тяжелее остальных, зависит от того, поднялась ли чаша весов с монетами 9, 10 и 11 или опустилась. Теперь возьмем любую из монет 9, 10, 11 и сравним вес двух из них, отложив третью монету в сторону (так же как мы сделали с девятью монетами в задаче Баше о взвешивании). В случае равновесия чаш весов оставшаяся монета – фальшивая. Если нам известно, что фальшивая монета легче, то она будет лежать в поднятой чаше. Если нам известно, что фальшивая монета тяжелее, то она лежит в опущенной чаше.

Решение несколько усложняется, если после первого взвешивания монет 1, 2, 3, 4 и 5, 6, 7, 8 весы не уравновешены.

Представьте себе, что чаша весов с монетами 1, 2, 3, 4 ниже чаши с монетами 5, 6, 7, 8.

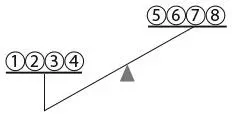
Следовательно, 9, 10, 11 и 12 – не фальшивые монеты.

Для второго взвешивания возьмем одну из правильных монет (например, монету 9) и поместим ее на чашу весов вместе с двумя монетами из той чаши, которая опустилась при первом взвешивании (скажем, вместе с монетами 1 и 2). Две оставшиеся монеты из опустившейся чаши (монеты 3 и 4) положим на другую чашу вместе с одной монетой из поднявшейся чаши (скажем, с монетой 5). Монеты с номерами 6, 7 и 8 не участвуют во взвешивании.

Вот три возможных итога второго взвешивания:

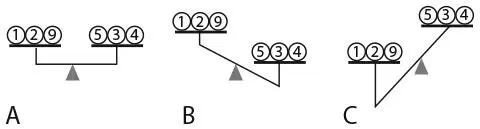
Вариант А. Весы уравновешены. Значит, фальшивая монета – это 6, 7 или 8. При третьем взвешивании сравните вес монет 6 и 7. Если весы уравновешены, фальшивой монетой будет 8, причем она легче остальных, поскольку чаша весов с ней поднялась при первом взвешивании. Если чаша весов с монетой 6 поднимется, то это и есть фальшивка, а если опустится, то наша правонарушительница – монета 7.