Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

К тексту

3. в) 3, д) 5.

Буква e уже встречается в предложении восемь раз, поэтому предложение будет верным, если на месте пробела поставить слова nine (9) и eleven (11).

К тексту

4. B.

В местах пересечения разорванная линия нарисована первой, а сплошная проведена поверх нее. Следовательно, нам нужно найти маршрут, на котором линия разрывается, проходя любое пересечение впервые, и не разрывается, когда проходит через соответствующее пересечение во второй раз. Этому условию удовлетворяет только маршрут, который начинается в точке B и направлен от точки D.

К тексту

5. в) 45 × 56.

Из предложенных вариантов выражения 23 × 34, 56 × 67 и 67 × 78 не делятся на 5, поэтому их можно исключить из рассмотрения. Кроме того, число 34 не делится на 4, а 45 – нечетное число, так что выражение 34 × 45 тоже можно исключить, поскольку оно не делится на 4. Единственный оставшийся вариант – 45 × 56. Если представить это выражение в виде простых чисел, получится 45 × 56 = 2 3× 3 2× 5 × 7. Очевидно, что это число делится на все целые числа от 1 до 10 включительно, так как у нас есть простые числа 2, 3, 5 и 7, а остальные числа можно образовать из этой совокупности простых чисел: 4 = 2 2, 6 = 2 × 3, 8 = 2 3и 9 = 3 2.

К тексту

6. б) 2.

Если валет червей говорит правду, то лжет валет треф. Это означает, что валет бубен говорит правду, а валет пик лжет. С другой стороны, если валет червей лжет, то правду говорит валет треф; тогда лжет валет бубен, а валет пик говорит правду. В обоих случаях мы можем сказать, что два валета лгут, хотя нет возможности определить, кто именно.

К тексту

7. б) 3.

В каждом углу куба сходятся три грани, причем каждая пара граней имеет общее ребро. Следовательно, необходимо три разных цвета. Другие цвета не понадобятся при условии, что противоположные грани окрашены в такой же цвет, поскольку противоположные грани не имеют общих ребер.

К тексту

8. б) 100.

Если мой возраст сейчас – x , то возраст бабушки – 4 x. Пять лет назад 4 x – 5 = 5( x – 5). Сокращаем уравнение до x = 20. Следовательно, моей бабушке 80 лет, а мне 20 лет.

К тексту

9. б) –1.

Сначала сосредоточимся на младших (крайних правых) цифрах указанных чисел, то есть на 3, 5, 7 и 9, так как именно их нужно прибавить или вычесть, чтобы получить число, оканчивающееся на 0. Мы видим, что цифра 3 появляется первой, и это хорошо. Но если 3 + 7 = 10, то из 5 и 9 нельзя получить число, оканчивающееся на 0. Следовательно, мы должны выполнить операцию 3–7. И в нашем выражении перед числом 67 должен стоять знак минус. В таком случае 123 – 67 = 56. Далее нам необходимо получить недостающее число 44 из чисел 45 и 89. Единственный способ сделать это – из 89 вычесть 45. В итоге правильное выражение выглядит следующим образом: 123 – 45–67 + 89. В нем два знака минус и один знак плюс, а значит, p – m равно −1.

К тексту

10. a) 1:1.

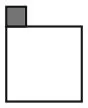
Мы можем рассматривать эту схему укладки плитки как мозаику, составленную из фрагментов показанной ниже формы, а значит, искомое соотношение – 1:1.

К тексту

Как и в задаче о сотне кур, нам необходимо представить условия в виде двух уравнений: для птиц и для денег. Если количество уток, голубей и кур обозначить x, y и z , то получим:

[1] x + y + z = 100;

[2] 2 x + y /2 + z /3 = 100.

Сначала умножим уравнение [2] на 6, чтобы избавиться от дробей.

[3] 12 x + 3 y + 2 z = 600.

Кроме того, умножим уравнение [1] на 2, чтобы в нем было 2 z.

[4] 2 x + 2 y + 2 z = 200.

Теперь нам осталось только записать одно уравнение, сократив член 2 z. Преобразовав уравнение [3], получим 2 z = 600 – 12 x – 3 y , а подстановка этого выражения в уравнение [4] даст следующее:

2 x + 2 y + 600 – 12 x – 3 y = 200.

Это уравнение можно привести к такому виду:

[5] 10 x + y = 400.

Нам известно, что x y – целые числа меньше 100. Кроме того, мы можем сделать вывод в отношении y : значение этой переменной должно быть кратным 10. Поскольку 400 делится на 10, другая сторона уравнения 10 x + y тоже должна делиться на 10. Мы также знаем, что 10 x делится на 10, а значит, значение y также должно быть кратным 10, иначе 10 x + y не делилось бы на 10, а это противоречит тому, что нам известно.

Числа меньше 100, кратные 10, – это 10, 20, 30, 40, 50, 60, 70, 80 и 90. Однако y не может иметь значение 70, 80 или 90, потому что тогда значение x было бы 33, 32 и 31, а сумма x и y превысила бы 100. Шесть искомых решений выглядят так: y = 10, 20, 30, 40, 50 и 60, что дает нам следующее распределение птиц: