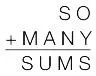Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

Если вы сделаете только один оборот, распутать струны посредством пропускания картона между ними будет невозможно. Но при двух оборотах переплетение можно распутать, какой бы способ вращения вы ни выбрали.

Пит Хейн считал, что решение этой головоломки доставит вам наибольшее удовольствие, если превратить ее в игру с двумя участниками; он назвал ее «Танглоиды». Один игрок держит левый конец модели, а другой – правый. Первый игрок делает два оборота своей картонки, а его визави должен распутать образовавшееся переплетение. Игроки меняются местами, а побеждает тот, кто быстрее распутает струны.

Самое удивительное свойство струнной модели в том, что переплетение, полученное в результате двойного оборота, всегда можно распутать, а образованное одним оборотом – нельзя; эта особенность помогает объяснить поведение определенных вращений в пространстве. Видимо, по этой причине данная модель интересовала Нильса Бора и его коллег. Британский физик Поль Дирак, проведший некоторое время в Копенгагене, использовал данную модель в качестве наглядного пособия для иллюстрации того факта, что «фундаментальная группа вращений в трехмерном пространстве имеет единственный генератор второго порядка».

Как вы уже убедились, порой хорошая головоломка похожа на фокус, а порой может служить блестящим объяснением серьезных научных концепций.

1. Сколько из приведенных ниже утверждений истинны?

Ни одно из этих утверждений не истинно.

Лишь одно утверждение истинно.

Лишь два утверждения истинны.

Все утверждения истинны.

Варианты ответов:а) 0; б) 1; в) 2; г) 3; д) 4.

Ответ

2. Какая из фигур не может образоваться при наложении двух одинаковых квадратов?

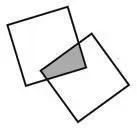
Варианты ответов:а) равносторонний треугольник; б) квадрат; в) дельтоид [33]; г) семиугольник; д) правильный восьмиугольник.

Ответ

3. Только одно из следующих уравнений верно? Какое именно?

Варианты ответов:

а) 44 2 + 77 2 = 4477;

б) 55 2 + 66 2 = 5566;

в) 66 2 + 55 2 = 6655;

г) 88 2 + 33 2 = 8833;

д) 99 2 + 22 2 = 9922.

Ответ

4. Сколько существует способов расположения в один ряд пяти переключателей во включенном или выключенном положении таким образом, чтобы никаких два соседних переключателя не находились в выключенном положении?

Варианты ответов:а) 5; б) 10; в) 11; г) 13; д) 15.

Ответ

5. В приведенной ниже записи сложения буквами обозначены разные цифры; буквой S обозначена цифра 3. Чему равно значение Y × O?

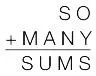
Варианты ответов:а) 0; б) 2; в) 36; г) 40; д) 42.

Ответ

6. Электронные часы показывают часы, минуты и секунды. Сколько раз за каждые 24 часа все шесть цифр меняются одновременно?

Варианты ответов:а) 0; б) 1; в) 2; г) 3; д) 4.

Ответ

7. Один из следующих кубов – наименьший куб, который может быть записан в виде суммы трех положительных кубов. Что это за число?

Варианты ответов:а) 27; б) 64; в) 125; г) 216; д) 512.

Ответ

8. В последовательности чисел каждый четвертый член представляет собой сумму трех предыдущих членов. Первые три члена – это −3, 0, 2. Какой по счету номер первого члена этой последовательности, превышающего значение 100?

Варианты ответов:а) 11-й; б) 12-й; в) 13-й; г) 14-й; д) 15-й.

Ответ

9. Страницы книги пронумерованы: 1, 2, 3… Для того чтобы пронумеровать все страницы, понадобится 852 цифры. Назовите номер последней страницы.

Варианты ответов:а) 215; б) 314; в) 320; г) 329; д) 422.

Ответ

10. На рисунке изображен единичный куб (то есть куб, длина ребра которого равна 1), окрашенный в голубой цвет. Предположим, что к каждой из его шести граней приклеены единичные кубы голубого цвета, образующие трехмерный крест. Сколько единичных кубов желтого цвета понадобится для того, чтобы оклеить все свободные грани этого креста?

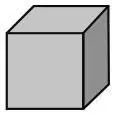
Варианты ответов:а) 6; б) 18; в) 24; г) 30; д) 36.