Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

Удастся ли вам доказать, что Пенни при любых обстоятельствах может собрать не меньшую сумму денег, чем Боб?

Подсказка: пронумеруйте монеты от 1 до 100.

Ладно, хватит уже игр с монетами! Давайте перейдем к головоломкам со спичками – этот предмет издавна занимает второе место по популярности в головоломках. Однако сначала предлагаю разобрать головоломку, в которой фигурируют и монета, и спички. Считайте ее эквивалентом редкого дуэта двух старых эстрадных певцов в области занимательной математики.

Ответ

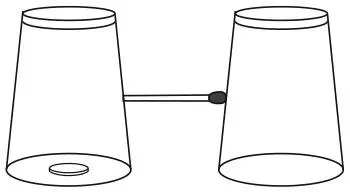
Два перевернутых стакана стоят так, как показано на рисунке. Между ними находится спичка; под левым стаканом лежит монета. Можете ли вы достать монету из-под стакана так, чтобы спичка не упала?

Спички были изобретены в XIX веке, и на протяжении сотни лет задачи со спичками были, пожалуй, самыми распространенными головоломками, которые решали представители разных поколений. Сейчас спички используются не так широко, как раньше, поскольку меньше людей курят, а у курящих, как правило, есть зажигалки. Приемлемой заменой спичкам могут стать зубочистки, карандаши или ватные палочки.

Генри Дьюдени называет следующую задачу «небольшой головоломкой для юных читателей».

Ответ

На рисунке изображено 16 спичек, которые образуют равносторонние треугольники.

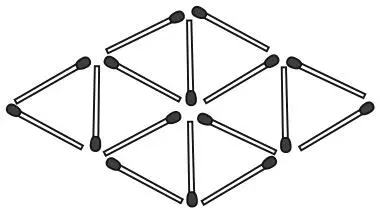
Уберите четыре спички так, чтобы осталось ровно четыре равносторонних треугольника и не было открытых концов и лишних спичек.

Ответ

Разложите 12 спичек в форме шестиугольника, состоящего из шести равносторонних треугольников.

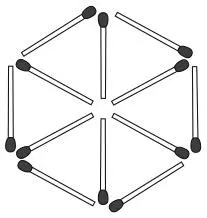
Эта головоломка решается за четыре шага.

1. Передвиньте две спички на другие места так, чтобы осталось пять равносторонних треугольников.

2. Теперь передвиньте две спички на другие места так, чтобы осталось четыре равносторонних треугольника. Не разрешается оставлять открытые концы, однако в следующих двух частях головоломки треугольники могут отличаться по размеру.

3. Передвиньте две спички на другие места так, чтобы осталось три равносторонних треугольника.

4. И наконец, проделайте то же самое так, чтобы осталось два равносторонних треугольника.

А теперь пойдем в противоположном направлении и увеличим количество треугольников. Мне очень нравится эта задача, потому что в ней совсем мало спичек.

Ответ

1. Перед вами два треугольника, составленных из шести спичек. Можете ли вы передвинуть две спички на другие места так, чтобы получилось четыре треугольника? Спички разрешается накладывать друг на друга.

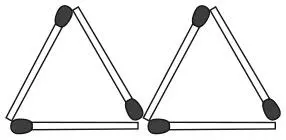
2. Теперь составьте четыре треугольника из шести спичек, не накладывая их друг на друга.

В одной из представленных выше головоломок нужно было разместить пять монет так, чтобы каждая монета соприкасалась со всеми остальными. Предлагаю вам ее другую версию – со спичками.

Ответ

В вашем распоряжении по-прежнему шесть спичек. Разложите их так, чтобы каждая спичка соприкасалась со всеми остальными. А теперь найдите способ сделать то же самое с семью спичками.

Расположение спичек, при котором они соприкасаются друг с другом только своими концами, можно воспринимать двумя способами: во-первых, как расположение спичек в определенном порядке, а во-вторых, как сеть точек, соединенных спичками, как показано в следующей головоломке.

Ответ

Найдите такое расположение двенадцати спичек, при котором оба конца каждой спички соприкасаются с концами двух других спичек. Иначе говоря, составьте сеть точек, соединенных спичками, в которой каждая точка связана с тремя другими.

В завершение игр со спичками давайте проанализируем следующий неожиданный аспект этой темы, на который обратил внимание наш старый друг Генри Дьюдени.

Ответ

На рисунке изображено 20 спичек, из которых построены две прямоугольные ограды, состоящие из 6 и 14 спичек соответственно. Площадь второго прямоугольника в три раза больше площади первого.