Тем более любопытно, что в главном опубликованном Ньютоном труде, «Математические начала натуральной философии», исчисление не упоминается вообще. Он посвящен изящному применению геометрии в стиле, заданном древними греками. Но внешность порой обманчива: неопубликованные документы, известные как «Портсмутские бумаги», доказывают, что во время работы над «Началами» Ньютон сформировал представление об идее исчисления. Очень похоже, что ученый использовал методы исчисления в большинстве своих открытий, однако предпочел не распространяться о них. Его наработки были опубликованы уже после его смерти, в книге «Метод флюксий и бесконечных рядов», в 1732 г.
Что такое исчисление? Метод, изобретенный Ньютоном и Лейбницем, проще понять, ознакомившись с более ранними идеями. Исчисление – это математика мгновенных изменений: насколько быстро изменяется определенная величина в это самое мгновение. Вот пример из физики: поезд движется по рельсам; как быстро он едет прямо сейчас? Исчисление делится на две главные ветви. Дифференциальное исчисление обеспечивает методы измерения скорости изменений и в большинстве случаев приложимо к геометрии, в частности при нахождении касательных к кривым. Интегральное исчисление подразумевает противоположное действие: исходя из скорости изменения некой величины, оно позволяет найти саму величину. Геометрические приложения интегрального исчисления включают способы вычисления площадей и объемов. Пожалуй, самым значительным открытием как раз и стала эта неожиданная связь между двумя внешне независимыми геометрическими вопросами: нахождение касательных к кривым и нахождение площадей.
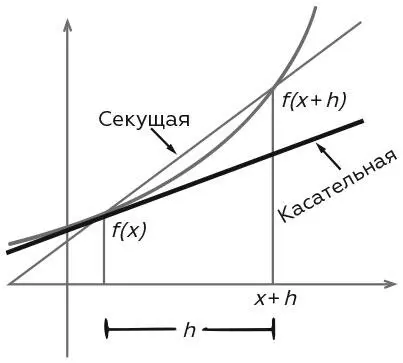
Геометрический смысл производной
Исчисление неразрывно связано с функциями – действиями, когда берется некое исходное число и определяется другое, связанное с ним. Как правило, такое действие описывается формулой, где данному числу, обозначенному как x (возможно, с некими дополнительными условиями), вводится в соответствие число f ( x ). В качестве примеров можно привести функцию квадратного корня f ( x ) = √x (в этом случае x должно быть неотрицательным числом) и квадратную функцию f ( x ) = x 2(в этом случае для x нет никаких условий).
Первой ключевой идеей исчисления является дифференцирование , т. е. взятие производной функции. Производная – это скорость изменения функции f ( x ), сравниваемая с изменением x , т. е. скорость изменения f ( x ) относительно x .
Геометрически скорость изменения – это тангенс угла наклона графика f в точке х . К нему можно приблизиться, определив угол наклона секущей – линии, пересекающей график в двух наиболее близких точках, соответствующих x , и x + h , где h невелико. Угол наклона секущей равен:
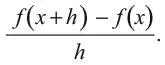
Теперь предположим, что h – очень малая величина. Тогда секущая приблизится к касательной на графике в точке x. Так что в определенном смысле необходимый угол наклона – производная f в точке x – будет пределом для этого выражения, поскольку h становится сколько угодно малым.
Попробуем произвести это вычисление для простого примера, f ( x ) = x 2. Получаем:
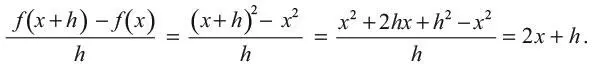
А поскольку h становится всё меньше, угол наклона 2 x + h всё ближе к 2 x . Производная f – это функция g , равная g ( x ) = 2 x .
Здесь главный концептуальный вопрос в том, что мы подразумеваем под пределом. У математиков ушел почти век на то, чтобы дать ему логичное определение.
Другой ветвью исчисления стало интегральное. Этот процесс проще всего представить как обратный дифференцированию. Интеграл g , описанный формулой
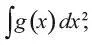
является любой функцией f ( x ), производная которой – g ( x ). Например, поскольку производная f ( x ) = x 2есть g ( x ) = 2 x , интеграл от g ( x ) = 2 x равен f ( x ) = x 2.
Читать дальше
![Йэн Стюарт Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres] обложка книги](/books/419776/jen-styuart-ukrochenie-beskonechnosti-istoriya-matema-cover.webp)

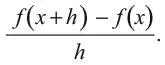
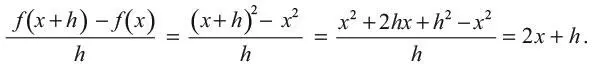
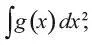





![Анна Одувалова - Высшая школа хаоса [litres]](/books/384215/anna-oduvalova-vysshaya-shkola-haosa-litres-thumb.webp)
![Ольга Пашнина - Богиня хаоса [litres]](/books/391340/olga-pashnina-boginya-haosa-litres-thumb.webp)
![Роджер Желязны - Владения Хаоса [litres]](/books/393502/rodzher-zhelyazny-vladeniya-haosa-litres-thumb.webp)
![Сара Бреннан - Дочь хаоса [litres]](/books/400527/sara-brennan-doch-haosa-litres-thumb.webp)
![Йэн Стюарт - Математика космоса [Как современная наука расшифровывает Вселенную]](/books/429584/jen-styuart-matematika-kosmosa-kak-sovremennaya-nau-thumb.webp)

