Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

Все числа хорошо совпадали, особенно если учесть ограниченные возможности астрономов того времени. Но существовало 120 различных способов разместить пять правильных тел, так что пространство в промежутках могло иметь разные размеры. Ничего удивительного, что один из этих вариантов оказался поразительно близок к реальности. Позже открытие новых планет нанесло роковой удар по всей теории, превратив ее в очередную тупиковую ветвь.

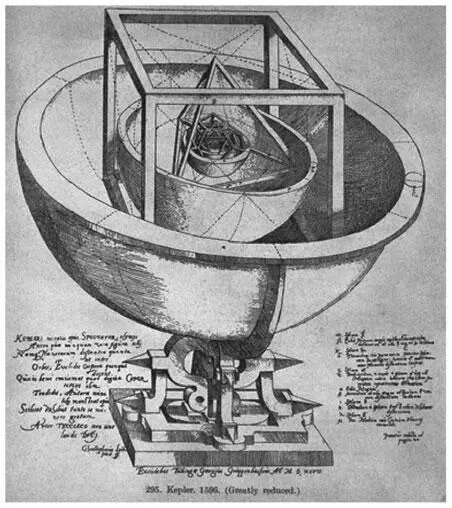
Теория Кеплера о расположении планетарных орбит

Однако в ходе своих исследований Кеплер открыл несколько законов, благодаря которым мы заслуженно считаем его гением. Эти законы Кеплера ученый установил интуитивно, исходя из анализа данных, собранных Тихо Браге. Вот как они звучат.

1. Все планеты Солнечной системы обращаются по эллипсам.

2. За равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.

3. Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей орбит планет.

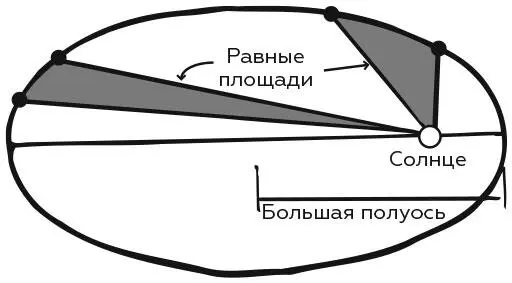
Движение планеты за равный промежуток времени

Самой оригинальной чертой работы Кеплера был отказ от классической окружности (якобы единственно возможной самой совершенной формы) в пользу эллипса. Этот шаг дался ученому с большим трудом, только когда он твердо убедился, что всё остальное не удовлетворяет его требованиям. У Кеплера не было оснований надеяться, что три закона будут точнее отражать реальность, чем гипотеза, основанная на платоновых телах, но это случилось. Три закона Кеплера имеют неоценимое значение для науки.

Следующей выдающейся фигурой той эпохи стал Галилео Галилей, открывший математические формулы движения маятника и падающих тел. В 1589 г., занимая должность профессора математики в Пизанском университете, он проводил эксперименты по качению шара по наклонной плоскости, но не опубликовал результаты. Однако именно тогда он осознал важность контролируемого эксперимента для изучения законов природы: эта идея стала фундаментальной для науки. Он занимался астрономией и сделал несколько важных открытий, побудивших его признать теорию Коперника о гелиоцентрической планетарной системе. Это обострило его отношения с церковью, обвинившей ученого в ереси и посадившей под домашний арест.

В последние годы жизни, уже окончательно ослабев здоровьем, Галилей создал «Беседы и математические доказательства двух новых наук», где объясняется его работа по движению тел на наклонных плоскостях. Он утверждал, что расстояние, на которое прокатится с постоянным ускорением изначально неподвижное тело, пропорционально квадрату времени. Основой его закона стало более раннее открытие, что снаряд летит по параболе. В сочетании с законами Кеплера о движении планет это заложило основу новой области науки – механики , математического описания движения тел.

Вот так и вышло, что физико-астрономические предпосылки привели ученых к исчислениям. Далее мы познакомимся с их математической основой.

Изобретение исчисления стало результатом более ранних исследований внешне не связанных проблем, обладавших скрытыми общими чертами. Сюда входит определение мгновенной скорости движения объекта в любой заданный момент, определение касательной к кривой, измерение длины кривой, определение максимального и минимального значения переменных величин, нахождение площади любой фигуры на плоскости и объема любого тела в пространстве. Ряд важных идей и примеров были разработаны Ферма, Декартом и не столь известным англичанином, Исааком Барроу, но методы решения по-прежнему оставались частными для каждой отдельной задачи. Требовался обобщенный поход.

Галилео был сыном Винченцо Галилея, преподавателя музыки, использовавшего эксперименты со струнами для подтверждения своей теории. В десять лет Галилео отдали на обучение в монастырь Валломброза с перспективой сделать его медиком. Но он не интересовался медициной и всё свое время посвящал математике и натуральной философии, которую позже мы назовем естественной наукой.