Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

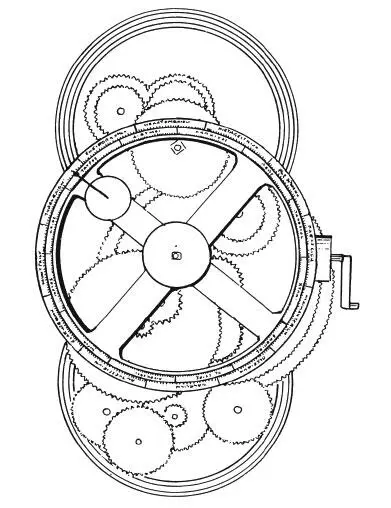
Антикитерский механизм и его реконструкция

Зубчатые колеса использовали еще древние греки для создания замечательного устройства – антикитерского механизма. В 1900 г. в окрестностях острова Антикитера ловец губок Элиас Стадиатис поднял с глубины 40 м бесформенную окаменелость, датированную примерно 65 г. до н. э. В 1902 г. археолог Валериос Стаис обнаружил, что в камне скрыты остатки зубчатого колеса и что на самом деле это часть сложного бронзового механизма. На нем были выгравированы слова, написанные буквами греческого алфавита. По имевшимся у ученых описаниям и форме объекта удалось определить, что это древний астрономический калькулятор. Он состоял минимум из 30 зубчатых колес (по последней реконструкции 2006 г. их было 37). Количество зубцов соответствовало основным астрономическим соотношениям. В частности, два колеса имели по 53 зубца – не самое простое число для изготовления детали. Оно соответствует частоте появления Луны на самом большом удалении от Земли по ходу ее орбиты. Все простые множители из числа зубцов были взяты из двух главных астрономических циклов: метонического и сароса. Рентгенологическое исследование выявило новые надписи и позволило их прочесть; теперь нет сомнений, что прибор использовался для определения положения Солнца, Луны и, возможно, всех известных тогда десяти планет. Эти надписи датируют 150–100 гг. до н. э.

Антикитерский механизм – сложнейший прибор, и, судя по всему, его создавали на основе теории Гиппарха о движении Луны. Вероятно, здесь не обошлось без участия его учеников. Также возможно, что прибор был игрушкой одного из членов царской семьи – судя по изощренности и дороговизне исполнения.

Третья важная тема «Исследований» – то самое открытие, которое подтолкнуло 19-летнего Гаусса посвятить всю свою жизнь математике: геометрическое построение правильного семнадцатиугольника (многоугольника с 17 сторонами). Евклид, использовавший линейку и циркуль, описал построение правильных многоугольников с тремя, четырьмя, пятью и пятнадцатью сторонами; он также знал, что эти числа сторон можно последовательно удваивать делением углов пополам, получая правильные многоугольники с шестью, восемью, десятью сторонами и т. д. Но Евклид не сумел построить многоугольники с семью или девятью сторонами – по сути, ни для одного числа, отличного от перечисленных выше. И на протяжении почти 2000 лет математики считали, что последнее слово осталось за Евклидом и невозможно построить иные правильные многоугольники. Гаусс опроверг это убеждение.

Легко заметить, что проблема в построении правильных p -угольников возникает, когда p – простое число. Гаусс указал, что построение такой фигуры подобно решению алгебраического уравнения:

x p – 1+ x p – 2+ x p – 3+ … + x 2+ x + 1 = 0.

Теперь, благодаря геометрии координат, построение с помощью линейки и циркуля может быть рассмотрено как последовательность квадратных уравнений. Если построение такого рода существует, оно следует правилу (не совсем тривиально), что p – 1 должно быть степенью 2.

Варианты древних греков, где p = 3 и p = 5, удовлетворяли этому условию: здесь p – 1 равно 2 и 4 соответственно. Но не только эти два простых числа удовлетворяют условию. Например, 17 – 1 = 16, тоже степень 2. Это еще не доказывает, что 17-угольник возможно построить, но дает серьезную зацепку, и Гауссу удалось найти блестящий способ сократить уравнение 16-й степени до последовательности квадратных уравнений. Он утверждал, хотя и не сумел доказать, что построение возможно для любого числа сторон p , если p – 1 составляет степень 2 (по-прежнему с условием, что p – простое число), и построение невозможно для всех других простых чисел. Доказательство вскоре было найдено другими учеными.

Эти особенные простые числа получили название чисел Ферма , потому что именно он их изучил. Он отметил, что если p – простое число и p – 1 = 2 k, то k само должно быть степенью 2. Он составил первую последовательность простых чисел Ферма: 2, 3, 5, 17, 257, 65 537. Он предположил, что числа вида 2 2 m+ 1 всегда простые, но это оказалось ошибкой. Эйлер открыл, что когда m = 5, то оно имеет множитель, равный 641.