Карл Левитин - Геометрическая рапсодия

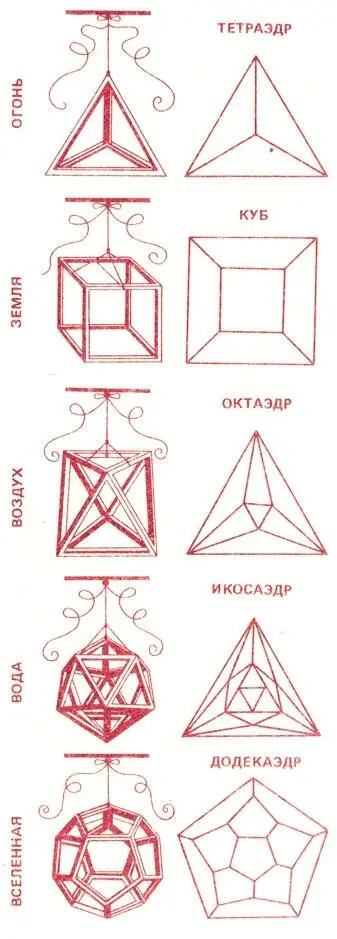
Что же божественного нашел в простых геометрических фигурах Лука Пачоли — человек, живший спустя два тысячелетия после Платона? Или это отзвук, прошедший через века и народы, приписываемой ему Плутархом крылатой фразы: "Бог всегда действует геометрически"?

Нет, фра Лука — монах Пачоли — мыслил реалистичнее: бог — геометр не всегда, но в некоторых случаях. А именно когда речь идет о "золотом сечении" — о таком делении отрезка на две неравные части, чтобы отношение большей части к меньшей равнялось отношению всего отрезка к большей его части.Завяжите простым узлом узкую полоску бумаги и осторожно распрямите его (12). Вы получите правильный пятиугольник, а его диагонали как раз и делят друг друга "в среднем и крайнем отношении" — так еще по-другому называют "золотое сечение". Пачоли нашел, что есть тринадцать "эффектов" этой "божественной" пропорции — "ради нашего спасения", как утверждал он. Он искал эти "божественные эффекты" в самых совершенных созданиях математики — пяти Платоновых телах, строил их из стеклянных плиток, а затем раздавал "для коллекций разных вельмож". В главе "О двенадцатом, почти сверхъестественном свойстве" речь идет о правильном икосаэдре — платоновом теле, ограниченном двадцатью правильными треугольниками.

Вглядитесь повнимательнее в эту древнейшую игральную кость (13). К каждой вершине сбегаются пять треугольников, свободные стороны которых образуют уже знакомый нам правильный пятиугольник. Если же соединить между собой любые два противоположные ребра икосаэдра, то получится прямоугольник, тоже имеющий прямое отношение к "божественной" пропорции, — его большая сторона так относится к меньшей, как сумма сторон — к большей. И именно икосаэдр связан с математической знаменитостью — проблемой "целующихся сфер", которая возникла в споре Исаака Ньютона с оксфордским астрономом Дэвидом Грегори (4).

Наконец, в самые последние годы это звучное греческое слово вновь замелькало в научных статьях: выяснилось, что структура кристаллического бора — идеальный икосаэдр. И даже вирусы, которые раньше так и назывались "сферическими" — например, вирус полиомиелита, — и то, как удалось обнаружить, имеют форму икосаэдра. Но об этом чуть позже.

"Евклид вовсе и не собирался выпускать систематический учебник геометрии. он задался целью написать сочинение о правильных многогранниках, рассчитанное на начинающих, в силу чего ему пришлось изложить все необходимые сведения" — шутка известного английского естествоиспытателя и геометра д'Арси Томпсона, как и всякая хорошая острота, содержит зерно истины. Ведь согласно Проклу, Евклид считал венцом всех тринадцати книг своих "Начал" предложенные им способы построения пяти Платоновых тел — недаром он поместил их в последнюю, тринадцатую книгу. Строить, в его понимании, значило начертить, пользуясь только циркулем и линейкой.

Но прежде чем браться за правильные пространственные тела, Евклиду пришлось "изложить все необходимые сведения" о правильных плоских фигурах.

В первой книге "Начал" он учит, как строить правильный треугольник, а в четвертой — квадрат, пяти-, шести- и пятнадцатиугольник с равными сторонами и углами при вершине. Но вот правильный семиугольник ни Евклиду" ни его последователям построить не удалось, а пытались многие, потому что семиугольная звезда играла определенную роль в астрологии. Однако только в 1796 году Карл Фридрих Гаусс сумел выяснить, какие именно правильные многоугольники могут быть построены с помощью циркуля и линейки, а какие — никогда. Ему было тогда всего 19 лет, и он готовился стать филологом. Открытая закономерность произвела на Гаусса такое сильное впечатление, что он не только забыл и думать о филологии, и не только с головой ушел в математику, но и всю жизнь, уже став великим ученым, гордился своим юношеским успехом. И геттингенцы поставили ему памятник, в пьедестале которого правильный 17-угольник. Сограждане великого математика достойно почтили его память. Установленный Гауссом закон связывает между собой две самые могучие ветви математического древа — геометрию и теорию чисел. ("Математика — царица наук, теория чисел — царица математики", — писал Гаусс.) Закон этот гласит: циркулем и линейкой можно построить правильный n-угольник в том и только в том случае, если число его сторон n разлагается на простые множители, каждый из которых является так называемым "простым числом Ферма", и вдобавок множители эти не повторяются. (Единственное исключение — числа, кратные 2. Они могут, конечно, входить в состав множителей n — ведь нетрудно сколь угодно раз удвоить число сторон уже построенного многоугольника.