Карл Левитин - Геометрическая рапсодия

Прогулка по зоологическому саду — не зоология в учебном смысле слова. Однако, мне кажется, что нужно сначала заинтересоваться животными, а потом уже заниматься их классификацией и анатомией. Сад открыт для всех, в том числе и тех, кто смотрит на животных только для развлечения. Поэтому не беда, если кто-нибудь скажет, что мои картинки — не математика. Кто пересмотрит их с начала до конца, тот, быть может, подметит то общее, что их объединяет. А это и есть математика...

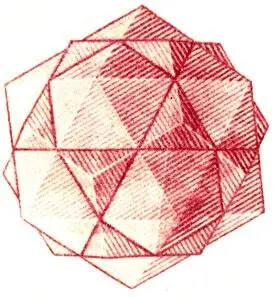
"Греки — это не способные школьники или хорошие студенты, но скорее "коллеги из другого колледжа", — писал профессор Джон Инденсор Литлвуд, один из крупнейших современных английских математиков. Поверим ему и не станем с насмешливым превосходством судить Платона за то, что он считал, будто атомы четырех элементов, из которых строится мир (огня, земли, воздуха и воды), имеют форму правильных выпуклых многогранников — тетраэдра, куба, октаэдра и икосаэдра, а весь мир в целом построен в форме додекаэдра. (На 73-й странице книги пять Платоновых тел сопоставлены с гравюрами Эсхера "Фейерверк", "Итальянский пейзаж. 1923", "Россано, Калабрия", "Второй день творения" и "Другой мир. 1947".) Воздержимся от саркастической улыбки и читая о "пятой сущности", или, по-латыни, "квинтэссенции" алхимиков, хотя их "колледж" чужд нам по духу. Подумаем лучше, почему именно додекаэдр, как показали раскопки в Монте Лоффа под Падуей, был любимой игрушкой этрусских детей 2500 лет назад? И почему он же до наших дней остается излюбленной побрякушкой для взрослых, которые делают из него календарь — по месяцу на каждый из двенадцати его граней (одно из изделий такого рода — брелок для ключей, изготовленный нашим "Автоэкспортом")?

Куб (или гексаэдр) и правильная пирамида (или тетраэдр) тоже верно служили большим и малым людям — и их созидательной тяге к строительству, и их разрушительной страсти азарта. Свидетельство тому — детские кубики и пирамидки, а также вся архитектура конструктивизма. Но почему же не куб и не пирамида, а совсем другой правильный многогранник — икосаэдр — хранится в Египетском зале Британского музея, и удивленный посетитель может узнать, что это — игральная кость династии Птолемеев? И почему октаэдр — "пространственный ромб" — от древних времен до наших дней неизменно служит светильником, хотя "начинка" его прошла путь от скоротечной плошки до почти вечной йодной лампы?

И наконец, главный вопрос: почему Платоновых тел (это математический термин) именно пять? Постарайтесь придумать шестое: выпуклый многогранник, каждая грань которого — один и тот же правильный многоугольник, то есть фигура с равными сторонами и равными углами между ними. Когда попытки ваши кончатся безрезультатно, попробуйте найти способ доказать себе и другим известное любому математику утверждение Евклида: существует только пять правильных выпуклых многогранников. И вне зависимости от успеха этого предприятия вы, вероятно, с большим пониманием, чем прежде, отнесетесь к словам профессора Литлвуда. И вне сомнения, с большим, чем в первый раз, интересом станете рассматривать гравюру Эсхера "Звезды", на которой среди прочих тел легко найти всю нашу "великолепную пятерку".

"Различные ветви геометрии находятся в тесных и часто неожиданных взаимоотношениях друг с другом" — такими словами Давид Гильберт предваряет одну из своих книг. Любой, в том числе и этот, рассказ о геометрии служит подтверждением их правдивости.

Леонардо да Винчи любил изготовлять из дерева каркасные модели многогранников. Когда его друг фра Лука Пачоли издал в 1509 году в Венеции книгу "О божественной пропорции", иллюстрациями к ней послужили пятьдесят девять рисунков, сделанных Леонардо со своих моделей. (Впрочем, Пачоли не остался в долгу: он подсчитал для великого скульптора количество металла, потребного для изготовления статуи всадника, — задача по тем временам нешуточная.)