Карл Левитин - Геометрическая рапсодия

Математика — это большой город, чьи предместья не перестают разрастаться, в то время как центр периодически перестраивается, следуя каждый раз все более ясному плану и стремясь к все более и более величественному расположению, в то время как... старые кварталы с их лабиринтом переулков сносятся для того, чтобы проложить к окраине улицы все более прямые, все более широкие и удобные...

"Униформа, по местам! Маэстро, туш!" — на арене фокусник. Его инструментарий прост до крайности — горизонтальная перекладина на двух стойках, в которую вбито несколько гвоздей, и на каждом из них висит по длинной яркой ленте. Все самое простое и настоящее — любой желающий волен убедиться в этом собственноручно. Маг закуривает сигарету и горящим концом дотрагивается до первой ленты. Пламя бежит вдоль нарисованной посередине ленты дорожки, вызывая восхищение малышей. Но вот огненное кольцо замкнулось — и тут уж крик удивления вырывается у взрослых: вместо ожидавшихся двух тонких лент появляется одна длинная. Прикосновение сигареты к другой ленте — снова взрыв детского восторга и за ним озадаченное молчание взрослых: теперь перед ними две ленты, продетые одна в другую. Еще одна огненная дорожка — и лента делает еще один неожиданный вольт: теперь она завязывается узлом.

Детская радость понятна — им неведомо, что на свете бывают химики и что они придумали калиевую селитру. Но и недоумение родителей тоже идет от незнания — топологии вообще и одной из ее излюбленных игрушек, "листа Мёбиуса", в частности.

А игрушка эта полюбилась математикам, и не им одним. У входа в Музей истории и техники в Вашингтоне медленно вращается на пьедестале стальная лента, закрученная на полвитка. В 1967 году, когда в Бразилии состоялся международный математический конгресс, его устроители выпустили памятную марку достоинством в пять сентаво. На ней была изображена все та же лента. И монумент высотой более чем в два метра, и крохотная марка — своеобразные памятники немецкому математику и астроному Августу Фердинанду Мёбиусу, профессору Лейпцигского университета.

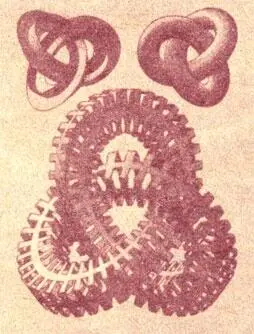
В своей работе "Об объеме многогранников" он описал геометрическую поверхность, обладающую совершенно невероятным свойством: она имеет только одну сторону! Самое же при этом удивительное, пожалуй, то, что сделать ее своими руками не представляет решительно никакого труда: надо лишь взять полоску бумаги и склеить ее концы, предварительно повернув один из них на 180 градусов. И тогда в ваших руках окажется лист, или лента, Мёбиуса. Чтобы наглядно убедиться, что у вашей самоделки действительно всего одна сторона, попробуйте закрасить перекрученную ленту в два цвета — одним с внешней, а другим — с внутренней стороны. Что бы вы ни придумывали, вам это не удастся. Но зато муравью, ползущему по листу Мёбиуса, не надо переползать через его край, чтобы попасть на противоположную сторону, как это видно на гравюре Маурица Эсхера "Лента Мёбиуса. II".

Итак, односторонность. В геометрическом, разумеется, понимании этого слова, потому что в нашем общечеловеческом смысле трудно представить себе более разностороннюю геометрическую фигуру. Теперь, когда вы познакомились с ней, наверное, уже никакая сила не Удержит вас от того, чтобы не клеить все новые и новые ленты, закручивая их то на один, то на два, а то и на три полуоборота, и потом беспощадно разрезать вдоль. И вы будете вознаграждены за свою любознательность — полоска бумаги повторит все фокусы, показанные в Цирке.

Да что цирк! Патентные службы вынуждены были познакомиться с поразительными свойствами листа Мёбиуса — в разное время и в разных странах зарегистрировано немало изобретений, в основе которых лежит все та же односторонняя поверхность. В 1923 году знаменитый американский изобретатель Ли де Форест, который придумал трехэлектродную лампу — триод, предложил записывать звук на киноленте без перемены катушек, сразу "с двух сторон". Ему выдали патент № 1442632. Изобрели магнитофон — и сразу же нашлись сообразительные люди, которые придумали особые кассеты, где магнитная лента соединяется в кольцо и перекручивается. Ясно, что тогда можно записывать и считывать подряд с двух дорожек, не снимая кассеты с магнитофона и не меняя их местами, а значит, время непрерывного звучания увеличивается ровно вдвое. (Речь идет, разумеется, о так называемой "непрерывной ленте", то есть замкнутой в кольцо, вроде автоматических телефонных часов или милицейских лозунгов о безопасности движения, передаваемых через репродукторы, патрульных машин.) В 1969 года советский изобретатель А. Губайдуллин получил авторское свидетельство № 236278 на бесконечную шлифовальную ленту, работающую обеими своими сторонами. Он предложил натянуть сделанную из специального материала ленту Мёбиуса на два вращающихся ролика и покрыть ее крупинками твердого абразива. Понятно, что такая лента служит вдвое больше обычной. Ту же идею использовали сотрудники НИИ автоматизации черной металлургии Г. Буйный и В. Изотов в своем устройстве для магнитной дефектоскопии (им выдано авторское свидетельство № 259449).