Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков

На риторические вопросы иногда даются риторические ответы, и этот конкретный вопрос, воспринятый всерьез, завел математиков в глухие интеллектуальные дебри. Первоначальной мотивацией служила одна из особенностей трактата «Начала» Евклида, в котором обнаружился недочет. Не ошибка, а всего лишь нечто, казавшееся недостаточно элегантным и в каком-то смысле лишним. Евклид организовал свое изложение геометрии последовательно, в логическом порядке, а начал с простых допущений, которые были сформулированы явно и не доказывались. Все остальное затем выводилось логически из этих допущений, шаг за шагом. По большей части допущения эти были просты и разумны: «все прямые углы равны между собой» [20] Евклид. Начала Евклида. – М., Л.: ГИТТЛ, 1948. , к примеру. Но одно из них было настолько сложным, что выделялось в общем ряду, как белая ворона в стае.

И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные неограниченно эти прямые встретятся с той стороны, где углы меньше двух прямых [21] Евклид. Начала Евклида. – М., Л.: ГИТТЛ, 1948. .

Это утверждение известно как аксиома (или постулат) о параллельных, потому что на самом деле речь здесь идет о параллельных прямых. Если две прямые линии параллельны, они никогда не пересекаются. В данном случае аксиома о параллельных гласит, что сумма внутренних углов в этом случае должна быть равна в точности удвоенному прямому углу – 180°. И наоборот, углы будут именно такими, если прямые параллельны.

Понятие о параллельных прямых фундаментально и очевидно: достаточно взглянуть на линованную бумагу. Представляется самоочевидным, что такие прямые существуют и они, разумеется, никогда не встретятся, потому что расстояние между ними всюду одинаково и, соответственно, не может стать нулевым. Евклид наверняка создал проблему на пустом месте, ведь все так очевидно! Возникло общее ощущение, что должна существовать возможность доказать аксиому о параллельных, используя остальные Евклидовы допущения. Мало того, некоторые (таких людей было несколько) были убеждены, что сделали это, но ни одно из подобных доказательств не выдержало проверки: независимые математики всегда обнаруживали в них ошибку или незамеченное спорное допущение.

Одну из первых попыток разрешить этот вопрос предпринял в XI в. Омар Хайям. Я упоминал его работу, связанную с кубическими уравнениями, но это был ни в коем случае не единственный его взнос в математическую копилку. Его «Комментарии к трудностям во введениях книги Евклида» построены на более ранней попытке Хасана ибн аль-Хайсама (в латинизированном варианте Альхазен) доказать аксиому о параллельных. Хайям логически отверг доказательство Ибн аль-Хайсама, как и другие «доказательства», и заменил их рассуждениями, в которых свел аксиому о параллельных к более интуитивно понятному утверждению.

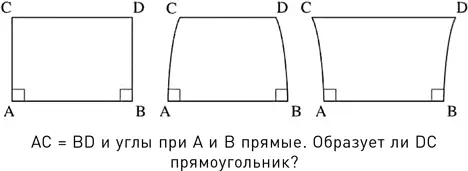
Один из ключевых чертежей Хайяма точно отражает суть проблемы. Его можно рассматривать как попытку построения прямоугольника – совершенно честную, можно сказать, попытку. Проводим прямую линию и строим под прямым углом к ней два отрезка прямых равной длины. Наконец, соединяем вторые концы этих отрезков, чтобы получить четвертую сторону прямоугольника. Готово!

Или нет? Откуда мы можем знать, что получившаяся в результате фигура – прямоугольник? В прямоугольнике все углы прямые, а противоположные стороны равны. На рисунке Хайяма мы видим, что два угла заведомо прямые и одна пара сторон одинакова. А что с остальными?

Да, согласен, все выглядит так, будто мы нарисовали прямоугольник, но это потому, что мы невольно пользуемся геометрией Евклида как мысленным ориентиром. И действительно, в Евклидовой геометрии мы можем доказать, что CD = AB и углы C и D тоже прямые. Однако этот вывод требует применения… той самой аксиомы о параллельных. Это едва ли можно считать удивительным, поскольку мы ожидаем, что CD будет параллельно AB. Если вы хотите доказать аксиому о параллельных на основании прочих аксиом Евклида, вам придется доказать, что Хайям нарисовал прямоугольник, не прибегая к аксиоме о параллельных. Более того, как понял Хайям, если вам удастся это доказать, дело будет сделано. Сама аксиома о параллельных напрямую из этого следует. Пытаясь избежать ловушки, связанной с попыткой доказать аксиому о параллельных, Хайям заменил ее на более простое предположение: «Две сходящиеся прямые пересекаются; невозможно, чтобы две сходящиеся прямые расходились в том же направлении, в каком они сходятся». И он вполне отчетливо понимал, что это действительно допущение.