Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков

Потребовалось немало времени, чтобы математики осознали правомерность неевклидовой геометрии и постигли ее значение. Процесс признания начался с выхода из печати французского перевода работы Лобачевского, сделанного Жюлем Оуэлем в 1866 г., через 10 лет после смерти автора. В глаза пытливому читателю бросалась одна важная вещь: отсутствие доказательства того, что отрицание аксиомы о параллельных никогда не приведет к противоречию. Понимание пришло несколько позже: на самом деле существует три непротиворечивые геометрии, удовлетворяющие всем остальным аксиомам Евклида. Во-первых, это сама Евклидова геометрия; во-вторых, это эллиптическая геометрия, где параллельные прямые попросту не существуют; и в-третьих, это гиперболическая геометрия, где параллельные прямые существуют, но не единственны.

Доказательство непротиворечивости оказалось проще, чем можно было ожидать. Неевклидова геометрия может быть реализована как естественная геометрия поверхности постоянной кривизны: положительной для эллиптической геометрии, отрицательной – для гиперболической. Евклидова геометрия представляет собой переходный случай нулевой кривизны. Здесь «прямая» интерпретируется в «геодезическом» смысле, как кратчайшее расстояние между двумя точками. В такой интерпретации все аксиомы Евклида, кроме аксиомы о параллельных, могут быть доказаны при помощи Евклидовой геометрии. Если бы в эллиптической или гиперболической геометрии имелась хоть одна логическая нестыковка, ее можно было бы непосредственно перевести в соответствующую логическую нестыковку в Евклидовой геометрии поверхностей. Но если Евклидова геометрия непротиворечива, то непротиворечивы и эллиптическая, и гиперболическая геометрии.

В 1868 г. Эудженио Бельтрами предложил конкретную модель гиперболической геометрии: внутренняя геометрия поверхности, известной как псевдосфера и имеющей постоянную отрицательную кривизну. Он интерпретировал этот результат как наглядное подтверждение того, что на самом деле гиперболическая геометрия не есть нечто новое; это просто Евклидова геометрия, приспособленная к соответствующей поверхности. При этом он упустил из виду более глубокий логический вывод: эта модель доказывает непротиворечивость гиперболической геометрии, так что аксиома о параллельных не может быть выведена из других аксиом Евклида. Оуэль понял это в 1870 г., когда перевел статью Бельтрами на французский.

Подобрать модель для эллиптической геометрии было проще. По существу, это геометрия больших окружностей на сфере, с одной оговоркой. Большие окружности пересекаются в двух диаметрально противоположных точках, а не в одной точке, и потому не удовлетворяют остальным аксиомам Евклида. Чтобы исправить ситуацию, достаточно переопределить «точку» как «пару диаметрально противоположных точек» и рассматривать большую окружность как пару диаметрально противоположных полуокружностей. Это пространство – формально сфера с попарно отождествленными противоположными точками – обладает постоянной положительной кривизной, унаследованной от сферы.

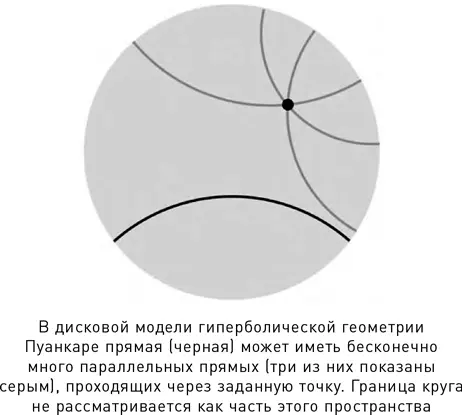
Тем временем неевклидова геометрия начала потихоньку появляться и в других областях математики, в первую очередь в комплексном анализе, где она связана с преобразованием Мёбиуса, отображающим окружности (и прямые) на окружности (и прямые). Вейерштрасс прочел лекцию на эту тему в 1870 г. Клейн, двигавшийся в том же направлении, уловил суть и обсудил эту идею с Софусом Ли. В 1872 г. он составил важный документ – Эрлангенскую программу, в которой определил геометрию как науку об инвариантах групп преобразований. Такой подход объединил почти все варианты, на которые успела разделиться к тому времени геометрия; основным исключением из этого перечня стала Риманова геометрия для поверхностей непостоянной кривизны, где подходящих групп преобразований просто нет. Пуанкаре зашел еще дальше, предложив, в частности, собственную модель гиперболической геометрии. Пространство в ней представляет собой внутренность круга, а «прямые» линии – дуги окружностей, подходящих к границе круга под прямыми углами.

Позже гиперболическая геометрия стала одним из стимулов к появлению Римановой теории искривленных пространств любой размерности (многообразий), на которой построена теория гравитации Эйнштейна (глава 15). В число ее приложений в современной математике входят комплексный анализ, специальная теория относительности, комбинаторная теория групп и гипотеза (теперь уже теорема) о геометризации Тёрстона в топологии трехмерных многообразий (глава 25).