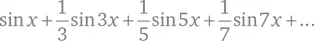Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков

В 1799 г. Наполеон бросил свою армию в Египте и возвратился в Париж. В 1801 г. Фурье последовал за ним и вернулся на свою профессорскую кафедру. Но Наполеон решил, что Фурье – слишком способный управленец, чтобы оставаться без дела, и предложил ему пост префектора департамента Изер. Это было предложение, от которого нерешительный Фурье был не в состоянии отказаться, и он переехал в Гренобль. Там он руководил осушением болот в Бургуэне, заведовал строительством новой дороги Гренобль – Турин и работал по приказанию Наполеона над объемным «Описанием Египта», опубликованным в 1810 г. В 1816 г. Фурье переехал в Англию, но вскоре вновь вернулся во Францию и стал постоянным секретарем Академии. Еще в Египте у него возникли проблемы с сердцем, которые продолжились и после возвращения во Францию; его мучили частые приступы удушья. В мае 1830 г. он упал с лестницы, в результате чего его состояние сильно ухудшилось, и вскоре после этого умер. Имя Фурье – одно из 72 имен, начертанных на Эйфелевой башне. Но если говорить только о математике, то важнейшим для Фурье стало время пребывания в Гренобле, поскольку именно там он осуществил свое грандиозное исследование по теплоте.

Тепловое уравнение Фурье описывает в символьном виде поток теплоты в теплопроводящем стержне – к примеру, металлическом. Если какая-то часть этого стержня горячее соседних с ней участков, тепло от нее распространяется на прилежащие области; если эта часть холоднее соседних участков, она нагревается за счет прилежащих областей. Чем больше разность температур, тем быстрее распространяется теплота. Скорость перетекания теплоты определяет также, насколько быстро охлаждается весь стержень целиком. Тепловое уравнение Фурье описывает, как все эти процессы взаимодействуют между собой.

Первоначально разные участки стержня могут быть нагреты или охлаждены до различных температур; таким образом создается температурный профиль распределения теплоты. Решения уравнения описывают, как начальное распределение теплоты вдоль стержня изменяется с течением времени. Точная форма уравнения привела Фурье к простому решению в одном частном случае. Если начальное распределение температуры представляет собой синусоиду, которая имеет максимум в центре, а к концам стержня сходит на нет, то с течением времени профиль температуры не меняется, а значение ее убывает и экспоненциально стремится к нулю. Однако Фурье хотел знать, что происходит с теплотой при произвольном начальном температурном профиле. Предположим, к примеру, что первоначально стержень нагрет на половине своей длины и охлажден на второй половине. Тогда начальный профиль представляет собой своеобразный меандр. Меандр – это не синусоида.

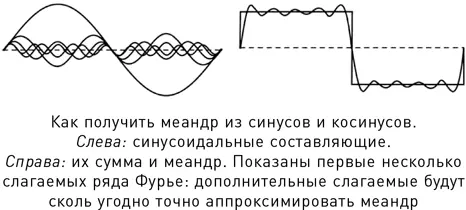
Чтобы получить решения несмотря на это препятствие, Фурье использовал важное свойство своего уравнения – его линейность. То есть любые два решения этого уравнения при сложении дадут еще одно решение. Если бы он мог представить начальный профиль как линейную комбинацию синусоид, то решение представляло бы собой соответствующую комбинацию экспоненциально убывающих синусоид. Он обнаружил, что меандр можно представить в таком виде, если взять бесконечное число синусоид и сложить профили вида sin x , sin 2 x , sin 3 x , sin 4 x и т. д. Чтобы получить точно прямоугольную форму, потребуется бесконечное число подобных слагаемых. Так, для стержня длиной 2π формула выглядит так:

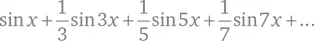
Красиво, не правда ли?

Расчеты убедили Фурье в том, что если использовать наряду с синусовыми и косинусовые слагаемые, то можно представить в виде бесконечного тригонометрического ряда любой начальный температурный профиль, каким бы сложным он ни был, даже если в нем имеются разрывы непрерывности, как в меандре. Поэтому и решение своего уравнения Фурье мог записать в той же форме. Каждое слагаемое убывает со своей скоростью; чем больше циклов колебания укладывается на синусоиде или косинусоиде, тем быстрее убывает соответствующая ей составляющая. Поэтому температурный профиль меняет не только размер, но и форму. Кроме того, Фурье методом интегрирования вывел общую формулу для слагаемых своего ряда.

Работа произвела на комиссию достаточно сильное впечатление, чтобы присудить ей приз, но членов комиссии встревожило заявление Фурье о том, что его метод применим к любому начальному профилю, даже если на нем будет множество скачков других разрывов непрерывности – как на меандре, только хуже. В качестве обоснования Фурье апеллировал к физической интуиции, но математики всегда опасаются, что интуитивные выводы и представления на самом деле могут основываться на каких-то неявно принимаемых предположениях. В самом деле, ни предложенный метод, ни возникающая в связи с ним проблема не были по-настоящему новыми. Тот же вопрос уже поднимался в связи с волновым уравнением и вызвал ссору между Эйлером и Бернулли; Эйлер опубликовал те же самые интегральные формулы разложения в ряд, что и Фурье, с более простым и элегантным доказательством. Главным различием было утверждение Фурье о том, что его метод применим к любым профилям, непрерывным или с разрывами, – утверждение, на которое Эйлер не решился. Для волн этот вопрос был не настолько серьезным, потому что прерывистый профиль был бы моделью порванной скрипичной струны, которая, естественно, колебаться не стала бы вообще. Но для распределения теплоты профили вроде меандра вполне могли иметь разумную физическую интерпретацию и потому тоже являлись объектом идеализированных модельных допущений. Но в остальном фундаментальная математика в том и другом случае была одна и та же, и на тот момент задача оставалась нерешенной.