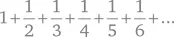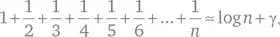Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков

Более простая бесконечная сумма, «гармонический ряд» обратных целых чисел, выглядит так:

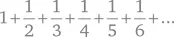
и расходится – его сумма бесконечна. Невозмутимый Эйлер нашел весьма точную приближенную формулу:

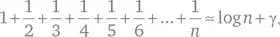
где γ, которую мы сегодня называем постоянной Эйлера, равна, до 16 знаков после запятой,

0, 577215664015328…

Эйлер сам вычислил ее значение с такой точностью. Вручную.

Теория чисел, естественно, привлекала внимание Эйлера. Он вдохновлялся в значительной мере примером Ферма, а дополнительную мотивацию давала его переписка с другом Гольдбахом, математиком-любителем. Решение базельской задачи привело его к замечательному соотношению между простыми числами и бесконечными рядами (глава 15). Он нашел доказательства нескольких фундаментальных теорем, сформулированных Ферма. Одной из них была так называемая Малая теорема Ферма, названная так, чтобы отличать ее от Великой теоремы Ферма. Эта теорема гласит, что если n – простое число и a не кратно n , то a n – a делится на n . Каким бы безобидным ни казалось на первый взгляд это утверждение, сегодня оно является основой для некоторых нераскрываемых, как считается, шифров, широко используемых в интернете. Кроме того, он обобщил результат для составного n , введя тотиент (или функцию Эйлера) ϕ( n ). Это число целых чисел между 1 и n , не имеющих с n общих простых делителей. Он предложил гипотезу о законе квадратичной взаимности, позже доказанную Гауссом (глава 10); описал все простые числа, представляющие собой сумму двух квадратов (2, все числа вида 4 k + 1, но не числа вида 4 k + 3), и улучшил теорему Лагранжа о том, что любое положительное целое число есть сумма четырех квадратов.

Учебники Эйлера по алгебре, математическому анализу, комплексному анализу и другим дисциплинам стандартизировали математическую запись и терминологию, значительная часть которой используется и сегодня (к примеру, π для числа «пи», e для основания натурального логарифма, i для корня квадратного из –1, Σ для суммы и f ( x ) для общего обозначения функции от x ). Он даже свел воедино системы записи Ньютона и Лейбница по дифференциальному исчислению.

Мне нравится определять математика не как «человека, который занимается математикой», но как «человека, который видит возможность применить математику там, где никто другой ее не увидел бы». Эйлер редко упускал такую возможность. Вот два примера, которые дали начальный толчок развитию новой области, известной сегодня как комбинаторика, или дискретная математика; область эта занимается счетом и упорядочиванием конечных объектов.

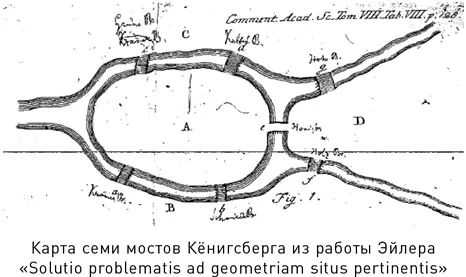
Первым из них в 1735 г. стала загадка, связанная с городом Кёнигсберг в Пруссии (ныне Калининград в России). В этом городе, расположенном на реке Прегель, имеется два острова, связанных друг с другом и с берегами реки семью мостами. Загадка состояла в том, чтобы найти такой маршрут через город, который прошел бы по каждому мосту ровно один раз. Начало и конец маршрута могли находиться в разных местах. Эйлер доказал, что такого маршрута не существует, а для этого рассмотрел более общий вопрос с любым расположением островов и мостов. Он доказал, что требуемый маршрут существует в том, и только том случае, когда не более чем два острова связаны с внешним миром нечетным количеством мостов. Сегодня мы интерпретируем эту теорему как одну из первых теорем теории графов – науки о сетях из точек, соединенных линиями. Доказательство Эйлера было алгебраическим и использовало символьное представление маршрута, где острова и мосты обозначались буквами. Несложно доказать, что сформулированное Эйлером условие необходимо для существования требуемого маршрута; труднее доказать, что этого достаточно для его существования.

Второй комбинаторной задачей, которую Эйлер поставил в 1782 г., была загадка 36 офицеров. Имеется шесть полков, в каждом из которых есть шесть офицеров шести разных званий. Можно ли построить полки квадратом 6 × 6 так, чтобы ни в одном ряду и ни в одной колонне не оказалось двух офицеров одного полка или одного звания? Эйлер предполагал, что это невозможно, но этому результату пришлось дожидаться доказательства Гастона Тарри до 1901 г. В основе решения здесь лежит латинский квадрат, в котором n экземпляров n символов необходимо разместить в квадрате n × n так, чтобы каждый символ в каждой строке и в каждом столбце встречался ровно один раз. Требуется, чтобы 36 офицеров образовали два «ортогональных» латинских квадрата – один для полка, другой для ранга, так, чтобы все возможные пары были в них включены. Латинские квадраты применяются, в частности, при разработке статистических тестов, а их широкие обобщения, известные как блочные планы, фигурируют в нескольких областях математики. Одна из вариаций на тему такого квадрата – головоломка судоку.