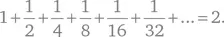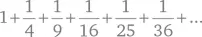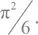В 1727–1730 гг. он служил также лейтенантом медицинской службы на Российском военном флоте, но затем, получив звание полного профессора, оставил флот и вскоре стал постоянным членом Академии. В 1733 г. Даниэль Бернулли оставил свою кафедру в Санкт-Петербурге, чтобы вернуться в Базель, и Эйлер стал его преемником на посту профессора математики. Его финансовое положение упрочилось достаточно, чтобы позволить себе женитьбу, и он без особого промедления связал себя узами брака с Катариной Гзелл – дочерью художника местной гимназии. С течением времени пара произвела на свет 13 детей, из которых восемь умерло во младенчестве; Эйлер как-то заметил, что лучше всего ему работалось с маленьким ребенком на руках и в окружении играющих детей.
Всю жизнь Эйлер испытывал хронические проблемы со зрением, обострившиеся в 1735 г. после сильнейшей лихорадки, от которой он чуть не умер. Как уже отмечалось, он тогда практически ослеп на один глаз. Это почти не повлияло на его научную продуктивность – на это вообще ничто никогда не влияло. Он выиграл большой приз Парижской академии в 1738 и 1740 гг.; всего он выигрывал этот приз 12 раз. В 1741 г., когда российская политическая жизнь стала слишком уж бурной, он переехал в Берлин и стал наставником племянницы Фридриха Великого. За 25 лет в Берлине он выпустил в свет 380 работ. Он писал книги по математическому анализу, по артиллерии и баллистике, по вариационному и дифференциальному исчислению, о движении Луны, орбитах планет, кораблестроении и навигации, написал даже научно-популярные «Письма немецкой принцессе».
Когда в 1759 г. умер Пьер Луи Моро де Мопертюи, Эйлер стал президентом Берлинской академии во всем, кроме формального титула, от которого отказался. Четыре года спустя король Фридрих предложил пост президента Жану ле Рон д’Аламберу, к которому Эйлер не испытывал особой симпатии. Д’Аламбер решил, что не хочет переезжать в Берлин, но дело было сделано, и Эйлер подумал, что ему пора сменить обстановку. В данном случае сменил он ее на прежнюю, поскольку вернулся по предложению Екатерины Великой в Санкт-Петербург, где и кончил свои дни, безмерно обогатив математику.
* * *
Почти невозможно убедительно рассказать о блестящем таланте Эйлера или о разнообразии и оригинальности его открытий в чем-то меньшем по объему, чем книга. Даже в этом случае это было бы непросто. Но мы можем бросить хотя бы один короткий взгляд на его достижения и проникнуться его замечательными способностями. Я начну с теоретической математики, а затем перейду к прикладной, не обращая внимания на хронологию, но стараясь выдерживать некоторую последовательность в развитии идей.
Во-первых и в-главных, Эйлер обладал поразительным чутьем на формулы. В своем «Введении в анализ бесконечно малых» 1748 г. он исследовал соотношение между экспоненциальной и тригонометрическими функциями для комплексных чисел, дающее формулу
e iθ = cos θ + i sin θ.
Отсюда, приняв θ = π радиан = 180°, можно вывести знаменитое уравнение
e iπ+1 =0,
связывающее две загадочные константы e и π и мнимое число i. Здесь e = 2, 718… является основанием натурального логарифма, а i – символ, который Эйлер ввел для корня квадратного из –1; он тоже широко используется и сегодня. Теперь, когда мы лучше понимаем комплексный анализ, это соотношение не кажется чем-то удивительным, но во времена Эйлера оно казалось сногсшибательным. Тригонометрические функции опираются на геометрию окружностей и измерения треугольников; экспоненциальная функция берет начало в математике сложного процента и опирается на логарифм как расчетный инструмент. Почему такие далекие друг от друга вещи должны быть так тесно, можно сказать интимно, связаны?
Сверхъестественное мастерство Эйлера в работе с формулами привело к триумфу и принесло ему великую славу в возрасте 28 лет, когда он решил базельскую задачу. Математики тогда активно искали интересные формулы для сумм бесконечных рядов, простейшей из которых, возможно, является формула
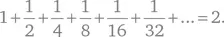
Базельская задача состояла в том, чтобы найти сумму обратных квадратов:
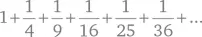
Многие знаменитые математики безуспешно пытались найти ответ на этот вопрос: Лейбниц, Стирлинг, де Муавр и трое самых искусных Бернулли: Якоб, Иоганн и Даниэль. Эйлер превзошел всех, доказав (или, по крайней мере, проведя расчет, на это указывающий, – строгость доказательств не была его сильной стороной), что эта сумма точно равна 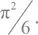
Читать дальше
Конец ознакомительного отрывка
Купить книгу