Владимир Арнольд - Теория катастроф

Прекрасные результаты теории особенностей, к счастью, не зависят от мрачной мистики теории катастроф. Но и в теории особенностей, как и во всей математике, есть нечто таинственное: это удивительные совпадения и связи между далекими на первый взгляд предметами и теориями.

Одним из примеров такого совпадения, остающегося загадочным (хотя кое-что и понято), является так называемая A, D, Е-классификация. Она встречается в таких разных отделах математики, как, например, теории критических точек функций, алгебр Ли, категорий линейных пространств, каустик, волновых фронтов, правильных многогранников в трехмерном пространстве и кристаллографических групп, порожденных отражениями.

Общим во всех этих случаях является требование простоты , или отсутствия модулей . Простота означает следующее. Каждая классификация есть разбиение некоторого пространства объектов на классы. Объект называется простым, если все близкие к нему объекты принадлежат конечному набору классов.

Пример 1 . Назовем два набора проходящих через точку 0 на плоскости прямых эквивалентными , если один из них переходит в другой при линейном преобразовании (х, у) → (ах + by, сх + dy). Любой набор трех прямых прост (любой набор трех различных прямых эквивалентен набору х = 0, у = 0, х + у = 0). Любой набор четырех проходящих через 0 прямых не прост (докажите!).

Пример 2. Будем классифицировать критические точки (комплексных) гладких функций, относя функции в один класс, если они сводятся одна к другой гладкой (комплексной) локальной заменой переменных. Список простых особенностей (скажем, для функций трех переменных) состоит из двух бесконечных серий и трех исключительных особенностей :

А k= х 2+ у 2+ z k+1, k ≥ 1;

D k= х 2+ y 2z + z k-1, к ≥ 4;

Е 6= x 2+ у 3+ z 4,

Е 7= x 2+ у 3+ yz 3,

Е 8= х 2+ у 3+ z 5.

Пример 3 . Колчаном называется набор точек и соединяющих их стрелок. Если каждой точке сопоставлено линейное пространство (точка, прямая, плоскость,...), а каждой стрелке — линейное отображение (соответствующего началу стрелки пространства в соответствующее концу), то говорят, что задано представление колчана . Два представления называются эквивалентными, если одно переходит в другое при подходящих линейных преобразованиях пространств.

Колчан на рис. 82 слева прост, справа непрост (см. пример 1).

Рис. 82. Простой и непростой колчаны

Оказывается, все связные простые колчаны получаются произвольной расстановкой стрелок на изображенных на рис. 83 диаграммах Дынкина, образующих две бесконечные серии и три исключительные диаграммы .

Простые особенности каустик и волновых фронтов также образуют две бесконечные серии А kи D kи три исключительные особенности Е k(начальные члены серий изображены на рис. 34 — 45).

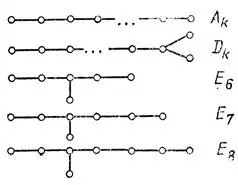
Рис. 83. Диаграммы Дынкина, определяющие простые колчаны

Группы симметрий правильных многогранников в трехмерном пространстве также образуют две бесконечные серии и три исключения (исключения — группы симметрий тетраэдра (Е 6), октаэдра (Е 7) и икосаэдра (Е 8), серии — группы правильного многоугольника и правильного диэдра, т. е. двустороннего многоугольника с окрашенными в разные или одинаковые цвета гранями).

На первый взгляд, функции, колчаны, каустики, фронты и правильные многогранники не связаны между собой. На самом деле соответственные объекты не случайно обозначены одинаково: например, из икосаэдра можно построить функцию х 2+ у 3+ z 5, а из нее — диаграмму Е 8, а также каустику и волновой фронт того же имени.

Легко проверяемым свойствам одного из соответствующих друг другу объектов соответствуют не обязательно очевидные свойства других. Таким образом, связи между всеми А, D, Е-классификациями используются для одновременного изучения всех простых объектов, несмотря на то, что происхождение многих из них (например, связей между функциями и колчанами) остается необъясненным проявлением загадочного единства всего сущего.

По словам поэта: