Владимир Арнольд - Теория катастроф

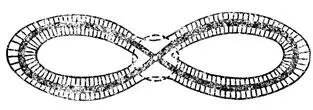
Рис. 78. Отождествление соседних множеств уровня функции вдали от критических точек

Отсюда следует, что монодромия, т. е. отождествление линий уровня с, непрерывно зависящее от пути, пробегаемого значением с при обходе критического значения, может быть выбрана так, что вне указанной окрестности все точки линии уровня вернутся на место, когда с совершит полный оборот.

Остается разобраться, что произойдет внутри окрестности. При этом достаточно рассмотреть стандартную функцию f = х 2+ у 2. Часть комплексной линии уровня, попавшая внутрь окрестности, топологически представляет собой цилиндр, оба края которого выходят на границу окрестности. В то же время эта часть двулистно накрывает область на плоскости комплексного переменного х с ветвлением в точках ± √c, как это объяснено выше (рис. 77).

Когда с совершает полный оборот вокруг нуля, отрезок между точками ветвления совершает пол-оборота, в результате чего мы возвращаемся к прежним (хотя и переставившимся) точкам ветвления. Непрерывно отождествляя между собой возникающие по дороге поверхности (так, чтобы точки краев оставались все время близкими к своему исходному положению), мы получим в конце концов отображение цилиндра на себя (монодромию), устроенное следующим образом.

Отрезок образующей цилиндра, обозначенный на рисунке 79, 1 буквой γ, в процессе отождествления переходит в кривые, обозначенные этой же буквой на промежуточных поверхностях (2, 3, 4). В конце концов мы возвращаемся к исходному цилиндру (5), но кривая у переходит в новую кривую с теми же концами. Легко сообразить, что на поверхности цилиндра эта новая кривая делает один полный оборот вдоль направляющей окружности, как и изображено на рис. 76.

Рис. 79. Построение монодромии последовательным отождествлением близких римановых поверхностей

Таким образом, монодромия перекручивает цилиндрическую часть комплексной линии уровня функции, расположенную вблизи критической точки, ровно на один целый оборот. Исчезающий цикл при таком перекручивании переходит в себя (повернувшись на π). Другие же циклы на линии уровня преобразуются в, вообще говоря, новые циклы. А именно, всякий раз, когда какой-либо цикл проходил вдоль образующей нашего цилиндра (т. е. пересекал исчезающий цикл), перекручивание изменяет проходящий цикл на исчезающий, так что (с точностью до непрерывных деформаций) образ проходящего цикла при монодромии получается из проходящего цикла добавлением столько раз взятого исчезающего цикла, сколько раз проходящий цикл (с учетом знаков) пересекал исчезающий. Если это число равно нулю, то проходящий цикл называется ортогональным исчезающему. Такой цикл при монодромии не меняется.

Мы вывели, таким образом (для функций двух переменных), "формулу Пикара — Лефшеца", основную в комплексной теории критических точек функций. При переходе к функциям любого числа n переменных исчезающий цикл становится сферой размерности n — 1, а цилиндр — множеством всех его касательных векторов. Если число переменных n нечетно, то монодромия действует на классы циклов как отражение в зеркале, ортогональном исчезающему циклу (сам он при монодромии меняет знак).

Сложные критические точки функций при общих малых шевелениях распадаются на простейшие. В результате общего малого шевеления возникает несколько критических значении и около каждого из них — по исчезающему циклу. Обход каждого из критических значений определяет преобразование монодромии. Подход от некритического исходного значения к каждому критическому значению по некритическому пути переносит исчезающий цикл в многообразие исходного неособого уровня пошевеленной функции. В результате там возникает целый набор исчезающих циклов.

Например, неособая комплексная линия уровня функции х 3+ у 2— это тор без одной точки. Малое шевеление х 3— εх + у 2имеет два критических значения (рис. 80). Подход к ним от некритической комплексной линии уровня определяет на этом торе два исчезающих цикла: параллель и меридиан тора. Точно так же на поверхности уровня функции х 3+ у 2+ z 2лежат две исчезающих сферы, пересекающиеся в одной точке. Соответствующие им преобразования монодромии — отражения пространства классов циклов в ортогональных исчезающим циклам зеркалах.