Владимир Арнольд - Теория катастроф

Переход системы на такой режим означает, что в ней наблюдаются сложные непериодические колебания, детали которых очень чувствительны к малому изменению начальных условий, в то время как усредненные характеристики режима устойчивы и не зависят от начального условия (при его изменении в некоторой области). Экспериментатор, наблюдающий за движением такой системы, назвал бы его турбулентным. По-видимому, неупорядоченные движения жидкости, наблюдаемые при потере устойчивости ламинарного течения с увеличением числа Рейнольдса (т. е. с уменьшением вязкости), математически описываются именно такими сложными аттракторами в фазовом пространстве жидкости. Размерность этого аттрактора, по-видимому, конечна при любом числе Рейнольдса (для двухмерных течений жидкости Ю. С. Ильяшенко, М. И. Вишик и А. В. Бабин недавно получили оценку этой размерности сверху величиной порядка Rе 4), но стремится к бесконечности при Re → ∞.

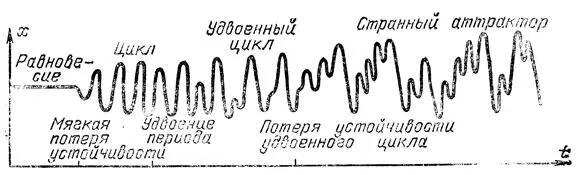
Рис. 20. Сценарий хаотизации

Переход от устойчивого состояния равновесия процесса ("ламинарного течения жидкости") к странному аттрактору ("турбулентности") может совершаться как скачком (при жесткой или катастрофической потере устойчивости), так и после мягкой потери устойчивости (рис. 20). В последнем случае родившийся цикл сам теряет устойчивость. Потеря устойчивости цикла в общем однопараметрическом семействе систем возможна несколькими способами: 1) столкновение с неустойчивым циклом (рис. 21), 2) удвоение (рис. 22), 3) рождение или смерть тора (рис. 23) (в терминологии Андронова: с цикла слезает шкура ). Детали последних процессов зависят от резонансов между частотами движения вдоль меридиана тора и вдоль его оси, т. е. от того, будет ли отношение этих частот рациональным или иррациональным числом. Интересно, что рациональные числа со знаменателем 5 и больше ведут себя практически как иррациональные.

Рис. 21. Гибель аттрактора-цикла

Поведение фазовых кривых, близких к циклу, можно приближенно описывать при помощи эволюционнсго процесса, для которого цикл является положением равновесия. Возникающие таким образом приближенные системы на сегодняшний день исследованы для всех случаев, кроме случаев, близких к сильному резонансу с отношением частот 1 : 4 (Р. И. Богданов, Э. И. Хорозов). На рис. 24 изображены перестройки семейства фазовых кривых приближенной системы, соответствующие перестройкам расположения фазовых кривых в окрестности цикла; предполагается, что потеря устойчивости происходит вблизи резонанса 1 : 3. На рис. 25 изображена одна из возможных последовательностей событий вблизи резонанса 1 : 4. Основные результаты об этом резонансе получены не строгими математическими рассуждениями, а комбинированием догадок и вычислительных экспериментов на ЭВМ (Ф. С. Березовская и А. И. Хибник, А. И. Нейштадт).

Рис. 22. Удвоение цикла-аттрактора

Изложенная выше теория Пуанкаре — Андронова потери устойчивости состояний равновесия имеет так много приложений во всех областях теории колебаний (как систем с конечным числом степеней свободы, так и сплошных сред), что нет никакой возможности их здесь перечислить: механические, физические, химические, биологические и экономические системы теряют устойчивость на каждом шагу.

Рис. 23. Бифуркация рождения тора вблизи цикла

В работах по теории катастроф мягкая потеря устойчивости положения равновесия обычно называется бифуркацией Хопфа (отчасти по моей "вине", так как, рассказывая о теории Пуанкаре — Андронова Р. Тому в 1965 г., я особенно подчеркивал работу Э. Хопфа, перенесшего часть этой теории на многомерный случай).

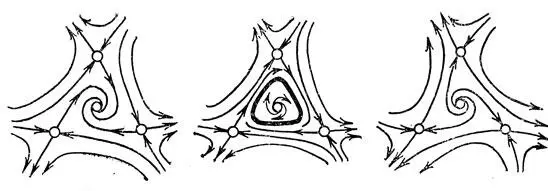
Рис. 24. Бифуркация коразмерности 2 вблизи резонанса 1 : 3

В теории бифуркаций, как и в теории особенностей, основные результаты и приложения получены независимо от теории катастроф. Несомненной заслугой теории катастроф является введение термина аттрактор и широкая пропаганда знаний о бифуркациях аттракторов. Разнообразные аттракторы обнаружены теперь во всех областях теории колебаний; высказывалась, например, гипотеза, что различные фонемы речи — это различные аттракторы звукообразующей динамической системы.