Владимир Арнольд - Теория катастроф

Системы, описывающие реальные эволюционные процессы, как правило, общего положения. Действительно, такая система всегда зависит от параметров, которые никогда не бывают известны точно. Малое общее изменение параметров превращает систему необщего положения в систему общего положения.

Таким образом, все более сложные, чем указанные выше, случаи, вообще говоря, не должны встречаться в природе, и их на первый взгляд можно не рассматривать. Эта точка зрения обесценивает большую часть теории дифференциальных уравнений и вообще математического анализа, где традиционно основное внимание уделяется малоценным, но трудным для исследования случаям не общего положения.

Дело, однако, обстоит совсем иначе, если нас интересует не индивидуальная система, а система, зависящая от одного или нескольких параметров. Действительно, рассмотрим пространство всех систем (рис. 12), разделенное на области, образованные системами общего положения. Поверхности раздела отвечают вырожденным системам; при малом изменении параметров вырожденная система становится невырожденной. Однопараметрическое семейство систем изображается на рис. 12 кривой. Эта кривая может трансверсально (под ненулевым углом) пересекать границу раздела разных областей невырожденных систем.

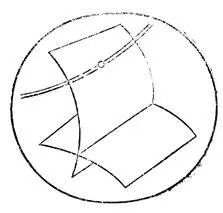
Рис. 12. Однопараметрическое семейство как кривая в пространстве систем

Таким образом, хотя при каждом индивидуальном значении параметра систему малым шевелением можно превратить в невырожденную, этого нельзя сделать одновременно при всех значениях параметра: всякая кривая, близкая к рассматриваемой, пересекает границу раздела при близком значении параметра (вырождение, устраненное малым шевелением при данном значении параметра, вновь возникает при некотором близком значении).

Итак, вырожденные случаи неустранимы, если рассматривается не индивидуальная система, а целое семейство . Если семейство однопараметрическое, то неустранимы лишь простейшие вырождения, изображаемые границами коразмерности один (т. е. задающимися одним уравнением) в пространстве всех систем. От более сложных вырожденных систем, образующих множество коразмерности два в пространстве всех систем, можно избавиться малым шевелением однопараметрического семейства.

Если мы интересуемся двупараметрическим семейством, то можно не рассматривать вырожденных систем, образующих множество коразмерности три и т. д.

Тем самым возникает иерархия вырождений по коразмерностям и стратегия их исследования: вначале следует изучать случаи общего положения, затем вырождения коразмерности один, затем — два и т. д. При этом исследование вырожденных систем не должно ограничиваться изучением картины в момент вырождения, но должно включать описание перестроек, происходящих, когда параметр, меняясь, проходит через вырожденное значение .

Изложенные выше общие соображения принадлежат А. Пуанкаре и применимы не только к исследованию положений равновесия эволюционных систем, но к большей части всего математического анализа. Хотя они были высказаны уже сто лет назад, успехи в реализации намеченной А. Пуанкаре программы теории бифуркаций остаются в большинстве областей анализа довольно скромными, отчасти в силу больших математических трудностей, отчасти же вследствие психологической инерции и засилья аксиоматико-алгебраического стиля.

Вернемся, однако, к положениям равновесия эволюционных систем. К настоящему времени решенным можно считать лишь вопрос о перестройках фазовых кривых при бифуркациях положений равновесия в однопараметрических семействах общего положения; уже случай двух параметров выходит за рамки возможностей сегодняшней науки.

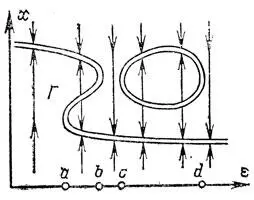
Рис. 13. Кривая равновесий однопараметрического семейства систем

Результаты исследования общего однопараметрического семейства суммированы на рис. 13 — 18. На рис. 13 изображено однопараметрическое семейство эволюционных процессов с одномерным фазовым пространством (по оси абсцисс отложено значение параметра ε, по оси ординат — состояние процесса х).