Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Эта весьма простая игра больше всего известна под названием Chomp [6] Звукоподражательное слово, передающее чавканье. Дело в том, что в эту игру можно играть на разделенной на дольки плитке шоколада: игрок, делающий очередной ход, отламывает и съедает те «клетки», которые он занимает по правилам игры. В русском варианте ( Гарднер М. Математические новеллы / Пер. с англ. Ю. А. Данилова. М.: Мир, 1974) игра называется «Щелк!». . Вариант этой игры на плитке шоколада изобрел ныне покойный американский математик Дэвид Гейл, а название Chomp придумал Мартин Гарднер. Играют в нее на разграфленной на клетки доске по следующим правилам.

Игрок, делающий первый ход, помечает одну из клеток крестиком.

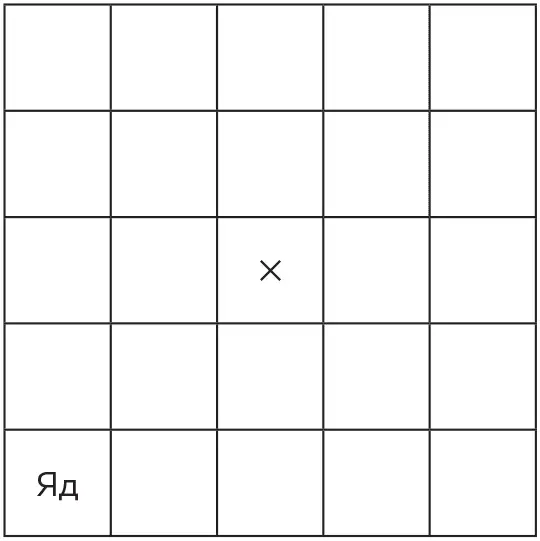
После этого все клетки, расположенные выше и правее помеченной, также помечаются крестиками (и выходят из игры). Ниже исходный крестик выделен жирным шрифтом:

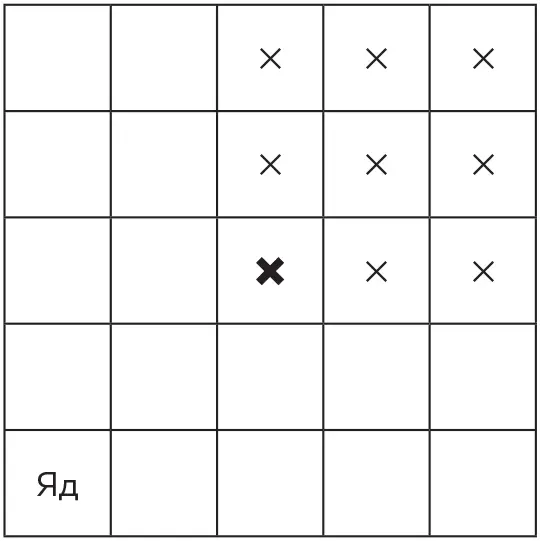
Теперь второй игрок должен пометить любую из оставшихся пустыми клеток ноликом. После этого все пустые клетки, расположенные правее и выше помеченной, также помечаются ноликами (исходный нолик выделен жирным шрифтом):

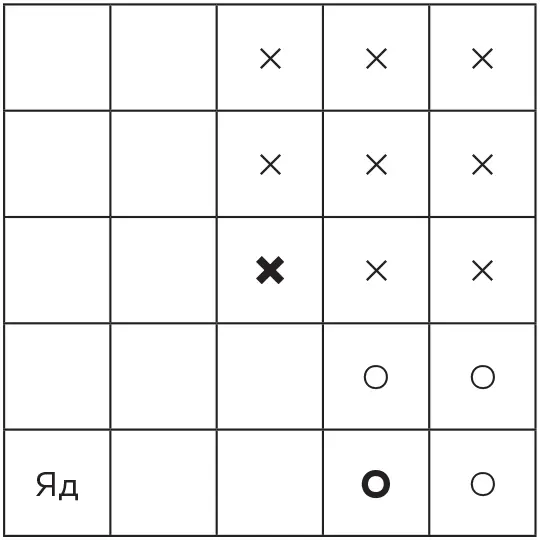
Затем первый игрок ставит следующий крестик, второй игрок ставит следующий нолик, и так продолжается до тех пор, пока один из них не будет вынужден съесть отравленную дольку и умереть (разумеется, метафорически).

Осторожно: эта игра затягивает!

Можете попробовать поиграть в нее на доске размером 7 × 4 (7 строк и 4 столбца или наоборот).

Если в эту игру играют на доске с равным количеством строк и столбцов, существует стратегия, при помощи которой первый игрок всегда побеждает. Можете ли вы ее найти? Подумайте минуты три.

Первый игрок должен выбрать клетку, расположенную по диагонали над ядом.

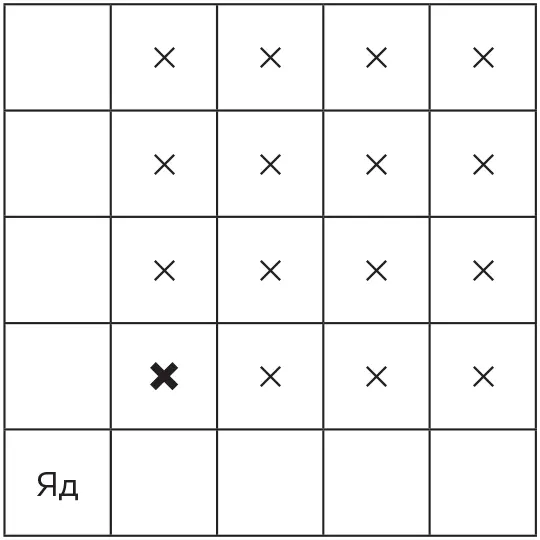
После этого все ответные ходы первого игрока должны быть симметричны ходам второго:

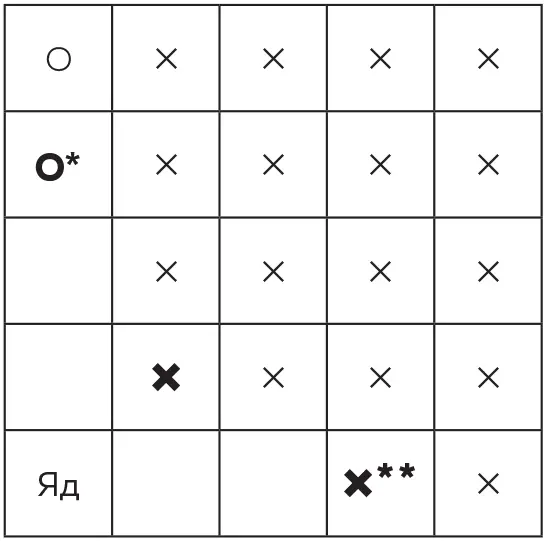
* Первый ход соперника

** Ответный ход первого игрока

Теперь должно быть ясно, как выиграть эту партию.

Ситуация становится гораздо более сложной, когда игра идет на доске, количества строк и столбцов на которой не равны; однако и в этом случае можно доказать, что для начинающего партию игрока существует выигрышная стратегия. К сожалению, доказательство не уточняет, в чем именно эта стратегия заключается. Математики называют такие доказательства «неконструктивными доказательствами существования».

И наконец, выполним упражнение.

Найдите выигрышную стратегию для первого игрока в игре на прямоугольной доске размером 2 × N (2 строки, N столбцов).

Подсказка: Чтобы получить симметричную позицию, как на квадратной доске, нужно прийти к положению, в котором незанятой останется только клетка с ядом или еще две клетки – одна над ядом и одна справа от него.

А теперь, когда вы (я надеюсь) решили эту задачу, что, по-вашему, произойдет, если на доске будут две строки и бесконечное количество столбцов? Кто выиграет теперь? Бесконечность – злостный нарушитель правил!

Я впервые услышал о Пифагоре, когда учился в 4 классе и записался в математический кружок – на внешкольные занятия, предназначенные для тех странных детей, которые любят проводить свое свободное время, изучая необычные геометрические фигуры и завязывая отношения с числами, в которых скрываются загадочные секреты. Мне нравилось даже произносить само это имя: Пи-фа-гор. Мне сразу же показалось, что человек с таким необычайно звучащим именем и сам должен быть личностью необыкновенной. И я не ошибся. Многие считают Пифагора (ок. 570 – ок. 495 г. до н. э.) одним из самых интересных философов досократовской эпохи. Еще «отец истории» Геродот (ок. 485 – ок. 425 г. до н. э.) называл Пифагора одним из величайших философов Древней Греции. Даже Гераклит (ок. 535 – ок. 475 г. до н. э.), философ чрезвычайно спесивый, сетовавший на глупость всего человечества (за исключением, разумеется, самого себя), признавал, что Пифагор свое дело знает.