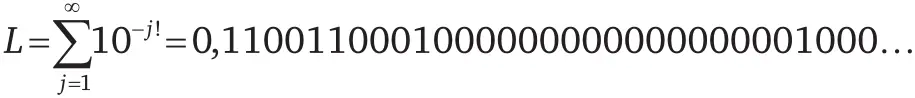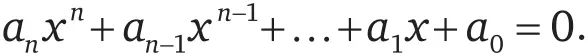Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Как мы уже сказали, в 1844 г. Лиувилль открыл одно трансцендентное число. Вот оно:

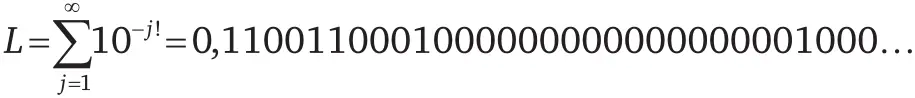
Вам может быть не вполне ясно, что именно это за число; позвольте мне объяснить.

Число Лиувилля строится следующим образом:

Шаг 1. Вычисляем все факториалы: 1! = 1, 2! = 2, 3! = 6, 4! = 24, 5! = 120…

Шаг 2. Составляем число, в котором после запятой встречаются только нули и единицы, причем 1 стоит на 1-м, 2-м, 6-м, 24-м, 120-м – и так далее – местах, а на всех остальных местах стоит 0.

Лиувилль доказал, что это число не является корнем какого бы то ни было алгебраического уравнения с целыми коэффициентами.

Как вы можете вообразить, это доказательство не слишком просто, так что вам придется поверить мне (и Лиувиллю) на слово – это действительно так.

Посмотрите на следующее число: 3,140001000000000000000005… сформированное сходным образом. Это число получено из десятичного представления числа π, в котором все цифры после запятой, кроме 1-й, 2-й, 6-й, 24-й, 120-й и так далее (их номера соответствуют 1! 2! 3!..), заменены нулями. На упомянутых же местах стоят последовательные цифры числа π.

Поскольку π =3,141592653589793… на 24-м месте оказывается цифра 5, на 120-м месте – цифра 9, на 720-м – цифра 2 и так далее.

Математики могут доказать, что это число также трансцендентно (а вам снова придется поверить, что они знают свое дело).

А как обстоит дело с самим π? Трансцендентно ли это число?

π : Я не рационально!

Вы не можете угадать, как я себя поведу…

Тот факт, что число π иррационально (то есть не существует такой дроби a / b , которая давала бы значение π), отметил – но не доказал – еще персидский математик, астроном и географ IX в. Мухаммад ибн Муса аль-Хорезми (в латинской транскрипции его имя передавалось как Algoritmi, и от него произошло слово «алгоритм»). Он был заметной фигурой знаменитого «Дома мудрости» в Багдаде в эпоху наивысшего расцвета исламской культуры. Ему принадлежит множество чрезвычайно важных достижений в области алгебры; более того, само слово «алгебра» происходит от сочетания «аль-джебр», взятого из названия фундаментального труда по этой науке, который аль-Хорезми написал около 820 г. [52] Этот труд назывался «Аль-китаб аль-мухтасар фи хисаб аль-джебр ва-аль-мукабала», что означает «Краткая книга восполнения и противопоставления». .

Маймонид также верил в иррациональность π, но не доказал его. Строгое доказательство получил только в 1768 г. швейцарский математик (Эйлер был не единственным швейцарским математиком!) Иоганн Генрих Ламберт.

Доказательство иррациональности числа π сравнительно просто; доказать же, что π – число трансцендентное, оказалось чрезвычайно трудно. Прошло еще более 100 лет, прежде чем немецкий математик Фердинанд фон Линдеман доказал в 1882 г., что π трансцендентно, то есть не является корнем какого-либо многочлена с целочисленными коэффициентами.

За несколько лет до этого, в 1873 г., французский математик Шарль Эрмит (вы заметили, как много нам встречается французских математиков?) доказал трансцендентность е – числа Эйлера {31} 31 Постоянная Эйлера е играет «главную роль» в самом красивом на свете равенстве e iπ + 1=0. Это число, равное 2,17181828459045… встречается в математике очень часто. Оно служит основанием натуральных логарифмов, используется в натуральной показательной функции, в вычислении процентов и в других областях. . Доказательство трансцендентности числа (особенно числа π) – процесс долгий и сложный, и здесь мы не станем входить в его подробности. В общем, просто представьте себе, каким образом можно получить доказательство того, что существует число, не дающее нуля ни в каком уравнении вида

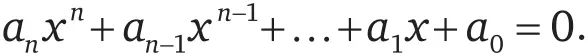
Это отнюдь не простая задача!

Чтобы проиллюстрировать ее сложность, скажу только, что в настоящее время все еще неизвестно, к каким числам – алгебраическим или трансцендентным – относится π в степени π (π π). Давид Гильберт (который, напомню, является счастливым «владельцем» бесконечной гостиницы) задавался вопросом об алгебраичности или трансцендентности числа 2 √2. Сегодня мы знаем, что это число трансцендентно. Собственно говоря, доказательство этого факта – часть общей теоремы, которая называется теоремой Гельфонда – Шнайдера, утверждающей, что число a b трансцендентно, если а – любое алгебраическое число, не равное 0 или 1, а b – иррациональное алгебраическое число. При помощи этой теоремы мы можем заключить, что е в степени π ( e π) должно быть трансцендентным, так как, если вы помните, e π = e i π(– i ) = (–1) – i .