Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Бесконечные множества чисел, которые невозможно расположить в последовательном порядке, называются – что и неудивительно – несчетными. Множество всех точек на числовой прямой, заключенных между 0 и 1, несчетно, и его мощность не равна ℵ 0. Следовательно, для обозначения мощности множества всех вещественных чисел (или любого отрезка прямой вещественных чисел) нужен новый символ! В качестве такого символа используют букву ℵ [50] В русской математической литературе чаще используется малая готическая . – Примеч. ред . Говорят, что ℵ – мощность континуума. Однако следует отметить, что несчетные множества не всегда имеют мощность ℵ.

Поскольку концепция канторовой диагонали не только красива, но и важна, я объясню ее еще раз – теперь на примере доказательства, что множество всех слов бесконечной длины, составленных с использованием только двух букв (a и b), невозможно подсчитать. Другими словами, такое множество несчетно.

Если вы уже поняли объяснение, которое профессор Финкельштейн-Островский-Канторович дал Омеге относительно чисел в десятичной системе счисления, у вас не должно вызвать затруднений и следующее изложение. Речь идет в точности о том же самом, только на другом примере. Если вы не вполне поняли первое объяснение, я надеюсь, что вы поймете его на этот раз.

Доказательство будет строиться от противного, то есть мы предположим, что справедлива противоположная гипотеза: все такие слова можно расположить в некой последовательности. Затем мы увидим, что это предположение приводит к противоречию, что означает, что наша исходная гипотеза была ложной.

Вот расположение слов:

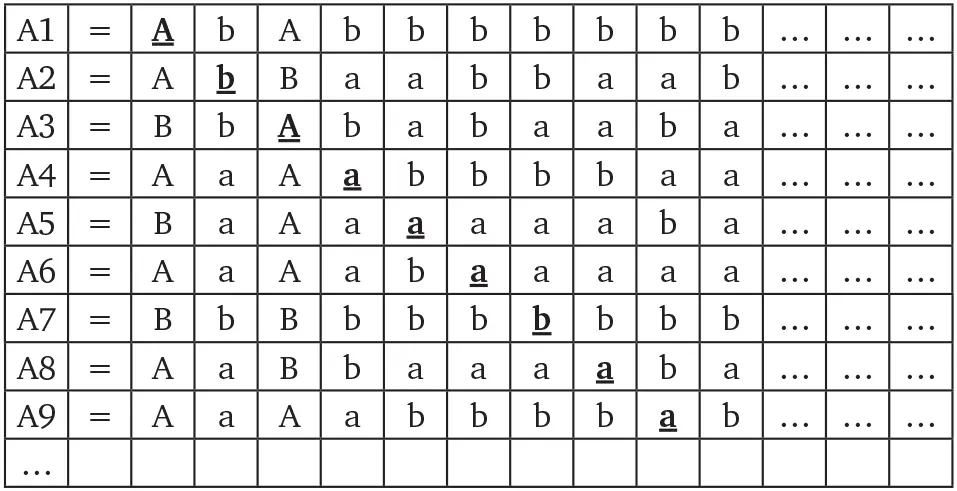
Применяя диагональный метод Кантора, аналогично тому, как мы действовали с числами, заключенными между 0 и 1, образуем новое слово А0, которое не содержится где бы то ни было в представленном в таблице множестве, в каком бы порядке мы ни располагали слова. Внимательно посмотрите на таблицу и обратите внимание на подчеркнутые буквы, стоящие на диагонали. Новое слово А0 будет построено следующим образом: его первая буква будет отличной от первой буквы слова А1 (поскольку первая буква в А1 – а, мы возьмем букву b); вторая буква будет отличной от второй буквы слова А2 (раз это буква b, мы используем букву а); третья буква будет отличной от третьей буквы слова А3 (на этот раз возьмем букву b) – и так далее.

Итак, наше новое слово A0 = babbbbabb…

Я предоставлю умудренному читателю самостоятельно убедиться, что слово А0 никоим образом не может встретиться в исходном бесконечном списке (то есть совпасть с каким бы то ни было его словом), потому что оно не может не отличаться от любого слова A i по меньшей мере буквой, стоящей на i -м месте.

К тому же, как уже выяснила Омега, добавление слова А0 в список ничего не меняет, потому что мы всегда можем повторить ту же процедуру и построить еще одно слово, назовем его Aℵ, которое будет отличаться от всех без исключения слов, включенных в составленный нами бесконечный список. Итак, множество всех слов бесконечной длины, содержащих только буквы a и b, имеет мощность континуума.

Очевидно, множество всех слов бесконечной длины, составленных с использованием трех разных букв (а не только букв a и b) или четырех или пяти (или любого другого количества) разных букв, также должно иметь мощность несчетного множества, что само по себе не означает, что его мощность будет равна мощности континуума. Однако, поскольку мы можем построить между таким множеством и множеством чисел, составленных из 0 и 1, одно-однозначное и сюръективное отображение, мы видим, что его мощность действительно равна ℵ.

Предположим, что верна противоположная гипотеза: все точки отрезка [0,1] можно пересчитать. Из этого следует, что все эти точки можно расположить в некотором последовательном порядке – {p 1, p 2, p 3, p 4…}. Чтобы доказать (или опровергнуть) эту гипотезу, возьмем вокруг центральной точки p 1отрезок длиной, скажем, 1/10, вокруг точки p 2 – отрезок длиной 1/100, вокруг точки p 3 – отрезок длиной 1/1000 и так далее. Поскольку все точки, содержащиеся на отрезке [0,1], попадают по меньшей мере на один из этих отрезков (вспомним, что в множестве {p 1, p 2, p 3, p 4…} были перечислены все числа, расположенные между 0 и 1), мы получаем множество, покрывающее весь отрезок [0,1]. А также можно сложить длины всех этих отрезков. В соответствии с формулой для бесконечной геометрической прогрессии: