Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Но что это?! Мы только что описали число n десятью словами (убедитесь сами), а следовательно, число n попадает в список чисел, которые можно описать, используя менее 1000 слов, что противоречит нашему определению этого числа.

Число n и Реджинальд Зевокк оказываются в этих двух парадоксах в одном и том же положении. Оба они определены как элементы некоторого списка, но затем их приходится исключать из этого списка в силу самого этого определения.

В чем проблема с этими двумя парадоксами? Математики терпеть не могут парадоксов и всегда ищут какое-нибудь объяснение, которое помогло бы им сохранить душевное спокойствие. Однако в этих случаях необходимо отметить, что мы использовали нематематическое свойство «можно описать», так и не дав его смыслу точного определения.

Это подводит нас к следующей теме нашего разговора.

Можно ли сказать, что некоторые числа более или менее интересны, чем другие?

Пифагор считал, что скучных чисел вообще не существует, что любое и каждое число чем-нибудь да интересно, что каждое число имеет по меньшей мере одно свойство, делающее его уникальным, или таит в себе нечто красивое или особенное.

А поскольку Пифагор придавал числам огромное значение, он стремился не только понять их с математической точки зрения, но и разглядеть в каждом из них красоту, загадку или тайну.

Какие именно характеристики числа делают его особенным или привлекательным? Это, по-моему, вопрос вкуса. «Привлекательна» ли принадлежность к совершенным числам? На мой взгляд, привлекательна. Мне также кажутся интересными пары дружественных чисел – эти числа по-настоящему умеют дружить. Было бы желание, а красоту можно найти в чем угодно – недаром говорят, что красота в глазу смотрящего.

Посмотрим, например, на число 64. В том факте, что 64 – квадрат 8 (8² = 64), нет ничего особенно выдающегося: многие другие числа тоже являются полными квадратами. Но число 64 может быть выражено и следующим образом: 64 = 2 6 = 4³.

Это уже гораздо интереснее. Оказывается (и это очень легко проверить), 64 – первое число (не считая 1), которое является не только квадратом (то есть второй степенью некоторого числа), но и третьей и шестой степенями.

Так что же, можем ли мы назвать 64 особенным числом? Поможет ли делу тот факт, что ему равно число клеток на шахматной доске? А еще в Камасутре описаны 64 позиции, а в «И цзин», китайской «Книге перемен», – 64 гексаграммы. Делает ли это число 64 хоть сколько-нибудь более выдающимся? Не знаю – решайте сами. А еще вы можете попробовать найти другие свойства, которые делают число 64 уникальным.

Предположим, нечто интересное есть в любом числе, и рассмотрим число 65, идущее сразу после 64. Можно ли найти что-нибудь замечательное в нем?

Разумеется, можно! Это число – второе в множестве натуральных чисел (после 50), выражаемое двумя разными суммами двух квадратов: 65 = 8² + 1² = 7² + 4². Кроме того , его еще можно выразить суммой двух кубов! 65 = 1³ + 4³. Более того, 65 – первое число, которое может быть выражено как суммой двух квадратов (причем двумя разными способами!), так и суммой двух кубов. Поразительно!

Сам Пифагор считал самым интересным число 36. Он полагал, что это идеальный возраст для мужчины (было ли у него какое-нибудь мнение об идеальном возрасте для женщины, я не знаю).

Математические свойства числа 36 впечатляли Пифагора, потому что:

36 = (1 + 2 + 3)² = 1³ + 2³ + 3³.

Когда я был моложе, я был согласен с Пифагором (и относительно вариантов выражения числа 36, и в том, что 36 лет – очень приятный возраст), но теперь я придерживаюсь более оптимистической точки зрения и считаю «идеальным возрастом» – как для мужчин, так и для женщин – 100 лет:

100 = (1 + 2 + 3 + 4)² = 1³ + 2³ + 3³ + 4³.

Те равенства, о которых мы только что говорили, далеко не случайны. Возможно, вы уже догадались, что квадрат суммы любого количества последовательных чисел равен сумме кубов всех этих чисел:

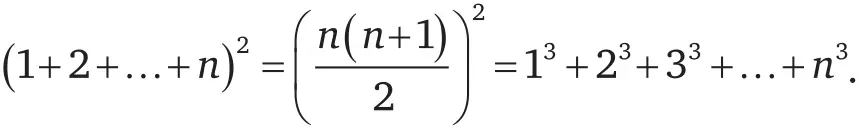
Мы обнаружили некоторые весьма интересные свойства некоторых чисел. Но наверняка существуют какие-то числа, в которых нет ничего по-настоящему уникального. Однако, если применить к числам парадокс «самого скучного человека на свете», то, может быть, число, не имеющее никаких особенных свойств, можно считать «интересным» именно этой особенностью.