Ю. Щербакова - Начертательная геометрия - конспект лекций

2) линия пересечения в точке К переходит с поверхности цилиндра 1 на верхнее основание цилиндра 3 (на плоскость 2).

Отрезок KLпрямой, по которой секущая плоскость пересечет плоскость 2, изображена в натуральную величину на плане ( KL = kl );

3) от точки L до точки R мы располагаем небольшой дугой эллипса, которая соответствует пересечению с боковой поверхностью цилиндра 3;

4) затем пересечение проходит по прямой RN , которая принадлежит плоскости 4 ( RN = rn );

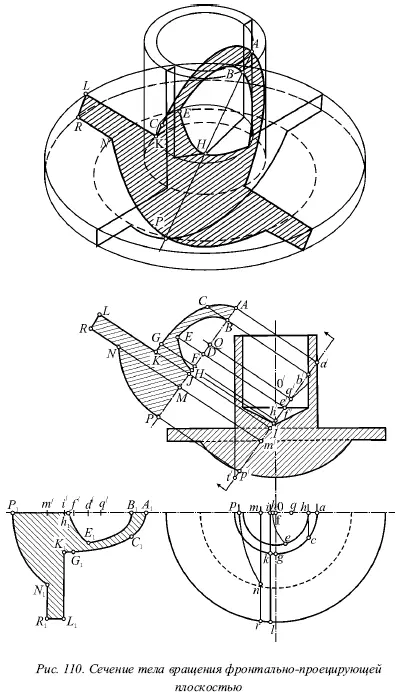
5) далее с плоскости 4 линия пересечения переходит на поверхность шара 5, центр которого находится в точке О , а центр окружности, по которой секущая плоскость пересекает поверхность шара, 1 в точке Q . При этом радиус этой окружности равен q́ṕ = QP , им нужно провести дугу из центра Q до встречи с прямой RM в точке N ( MN = mn );

6) соответственно от пересечения секущей плоскости с поверхностью цилиндра 6 должна получиться дуга эллипса BE . Здесь цилиндры 1 и 6 имеют общую ось, вследствие чего у обоих эллипсов один и тот же центр находится в точке F ;

7) линия пересечения переходит в точке Е на поверхность конуса 7, тогда наклон секущей плоскости по отношению к основанию конуса оказывается больше наклона образующей. Следовательно, мы получаем гиперболу с вершиной в точке Н , а слева от горизонтальной проекции на рисунке 110 построен натуральный вид этого сечения.

Чтобы найти следы прямой на поверхности некоторого геометрического тела, нужно провести через прямую вспомогательную плоскость, затем найти сечение поверхности тела этой плоскостью. Искомыми будут точки пересечения найденного сечения и данной прямой (рис. 111).

Для нахождения точек М и N , в которых прямая I встречает поверхность пирамиды, проделаем следующее.

1. Через данную прямую I нужно провести фронтальнопроектирующую плоскость Р .

2. Затем найти точки А 1, В 1и С 1, в которых ребра пирамиды встречают плоскость Р . Вследствие этого получим треугольник сечения поверхности пирамиды плоскостью Р.

Прямая I и треугольник А 1 В 1 С 1лежат в одной и той же плоскости Р, поэтому точки М и N пересечения прямой I со сторонами треугольника А 1 В 1 С 1являются искомыми.

Пусть нужно найти точки М и N , в которых прямая I встречает поверхность конуса. Для этого рассмотрим рисунке 112, на котором показано нахождение следов прямой на поверхности конуса. Через вершину S и данную прямую I проводят плоскость Р , что показано на рисунке 112, б, причем плоскость Р будет пересекать конус по двум образующим: AS и BS . Упомянутые образующие встретят данную прямую в искомых точках М и N . Тогда найдём проекции точек пересечения (рис. 112, а):

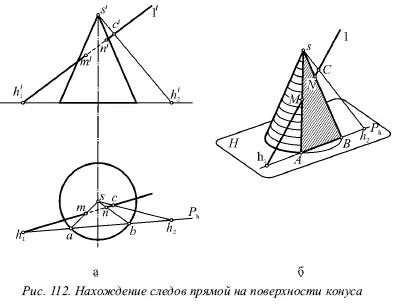
1) плоскость Р определяется точкой S и прямой I, тогда найдем ее след Р h. При этом одна точка следа P hопределяется следом h 1прямой I. Вторая точка искомого следа P hнаходится путем проведения в плоскости Р произвольной прямой до встречи с горизонтальной плоскостью. С этой целью соединим точку S с любой точкой С этой прямой и найдем след h 2прямой SC . Прямая, соединяющая точки h 1и h 2, будет представлять собой след P h;

2) затем нужно приступать к нахождению горизонтальных проекций а и b точек пересечения А и В следа P hс окружностью основания конуса;

3) после этого проводят горизонтальные проекции as и bs , образующих AS и BS , причем их фронтальные проекции не нужны;

4) далее отмечают точки пересечения m и n горизонтальных проекций образующих as и bs с горизонтальной проекцией данной прямой, они будут горизонтальными проекциями искомых точек М и N ;

5) в заключение остается найти фронтальные проекции ḿ и ń на фронтальной проекции Í данной прямой.