Ю. Щербакова - Начертательная геометрия - конспект лекций

Анализируя рисунок 108, заметим, что фронтально-проецирующая плоскость может давать сечения всех рассмотренных выше видов.

Любое сечение поверхности шара плоскостью является окружностью, которая проецируется без искажения только в том случае, если секущая плоскость параллельна плоскости проекций. В общем же случае мы будем получать эллипс. В том случае, если секущая плоскость перпендикулярна плоскости проекций, на этой плоскости проекцией окружности является отрезок прямой, который равен диаметру этой окружности.

На рисунке 109 показано пересечение поверхности шара горизонтально-проектирующей плоскостью Р . На горизонтальную плоскость сечение будет проецироваться в виде отрезка проекции р плоскости Р , который заключён между контуром шара и равен диаметру окружности сечения. На фронтальной плоскости мы получим эллипс. О 1является центром окружности, который получен в сечении шара. Он расположен на одной высоте с центром шара О . Горизонтальная проекция о 1центра О 1окружности располагается посредине отрезка ab . Перпендикуляр, который опущен из точки о на прямую ab , попадает в точку о 1, являющуюся горизонтальной проекцией центра окружности сечения. Фронтальная проекция о́ 1центра окружности является центром интересующего нас эллипса.

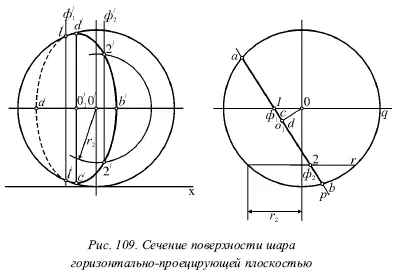
Если рассматривать эллипс как проекцию некоторой окружности, то его большая ось всегда будет проекцией того диаметра окружности, который параллелен плоскости проекций, а малая ось эллипса будет представлять собой проекцию диаметра, перпендикулярного ему. Вследствие этого большая ось эллипса проекции всегда равна диаметру проецируемой окружности. Здесь диаметр окружности CD перпендикулярен плоскости Н и проецируется без искажения на фронтальную плоскость. Для нахождения концов большой оси эллипса необходимо отложить вниз и вверх от центра о 1эллипса (по перпендикуляру к прямой о́о́ 1) отрезки о́ 1 с́ и о́ 1 d́ , которые равны половине диаметра окружности сечения о́ 1 с́ = о́ 1 d́ = 1/2( ab ). При этом диаметр АВ окружности параллелен горизонтальной плоскости, а его фронтальная проекция а́b́ представляет собой малую ось рассматриваемого эллипса.

Точки, отделяющие видимую часть эллипса от невидимой.Начнем с проведения фронтальной плоскости Q , которая делит шар пополам. Плоскость Q будет пересекать поверхность шара по окружности, проецирующейся на фронтальную плоскость в виде контура. Тогда часть линии сечения, расположенную на передней части шара, будет видно, если смотреть на шар спереди, а остальная её часть не будет видна. Плоскость Q пересечет плоскость Р по фронтали Ф 1. Пересекаясь с контуром, ее фронтальная проекция Ф определит точки 1 , которые отделяют видимую часть кривой от невидимой. Промежуточные точки 2́ эллипса можно найти с помощью вспомогательной фронтальной плоскости R, пересекающей поверхность шара по окружности радиуса r 2, а плоскость Р – по фронтали Ф 2.

Пусть требуется построить натуральный вид сечения фронтально-проецирующей плоскостью тела. На рисунке 110а рассматривается тело, ограниченное тремя цилиндрическими поверхностями (1, 3 и 6), поверхностью конуса (7) и сферой (5). При этом цилиндры 1 и 6 ограничены сверху плоскостью 8, а цилиндр 3 ограничен с двух сторон плоскостями 2 и 4. Следовательно, кроме кривых поверхностей, тело также ограничено тремя плоскостями (2, 4 и 8), причем плоскость 8 не затрагивается секущей плоскостью.

На рисунке 110б показана фронтальная проекция сечения, которая совпадает со следом плоскости. Построим натуральную величину сечения, ограничиваясь лишь одной его половиной.

Построение делают следующим образом:

1) цилиндр 1 пересекается секущей плоскостью по дуге эллипса, большая полуось которого имеется без искажения на главном виде áf́ . Здесь центр эллипса располагается на оси симметрии главного вида (точка f́ ), а отрезок FG является малой полуосью эллипса, которая равна радиусу окружности рассматриваемого цилиндра 1.

Для дуги этого эллипса в сечении мы строили четыре точки: А – конец большой оси (вершина эллипса), G – конец малой оси, С – промежуточная точка и К – точка, в которой заканчивается дуга эллипса;