Ю. Щербакова - Начертательная геометрия - конспект лекций

При пересечении поверхности тела вращения плоскостью Р обычно получают в сечении некоторую кривую линию. Основными задачами являются определение проекции линии, строение натурального вида сечения и развертка рассеченной поверхности тела вращения.

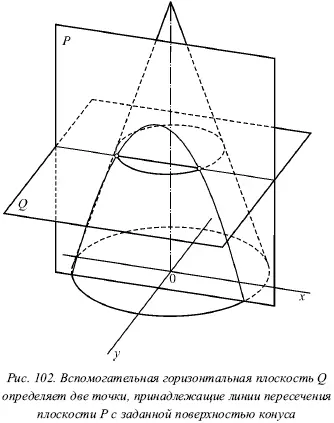
Как правило, кривая линия, полученная в сечении данного тела плоскостью, относится к лекальным кривым. Значит, для точного ее построения необходимо довольно много точек. Чтобы найти точки кривой, применяют метод проведения вспомогательных плоскостей. На рисунке 102 изображен конус, поверхность которого пересекается некоторой фронтальной плоскостью Р . Для получения нескольких точек, которые принадлежат линии сечения (гиперболе), нужно провести вспомогательную горизонтальную плоскость Q . Данная плоскость будет пересекать конус по окружности, а плоскость Р – по прямой линии. Точки, в которых полученная прямая пересекает окружность, принадлежат искомой линии пересечения.

Проведя таким же образом еще несколько вспомогательных горизонтальных плоскостей, будем получаться каждый раз по две точки искомой линии. При получении достаточного числа таких точек, следует соединить их плавной кривой, которая будет являться проекцией искомой линии пересечения.

Следовательно, метод проведения вспомогательных плоскостей заключается в нижеследующем.

1. Проводят вспомогательную плоскость Q так, чтобы линию пересечения ее с данной поверхностью можно было легко построить.

2. Приступают к построению этой линии, а также прямой пересечения плоскостей Р и Q , где Р является данной секущей плоскостью. Здесь общие точки линий пересечения плоскости Q с поверхностью и с данной плоскостью Р относятся к искомому сечению.

3. Выполнив несколько вспомогательных плоскостей, определяют необходимое количество точек сечения таким образом, чтобы искомую кривую можно было строить с помощью лекала.

Для поверхностей вращения любая плоскость, перпендикулярная оси вращения, будет пересекать данную поверхность по окружности. При выполнении чертежа все построения, связанные с нахождением отдельных точек кривой, нужно тонко выполнять карандашом, а после обводки кривой тушью вспомогательные построения удаляются. Благодаря этим линиям можно понять способ получения отдельных точек.

Построение развертки в этом случае возможно только в тех отдельных случаях, когда поверхность относится к числу развертывающихся, т. е. таких поверхностей, которые, будучи разрезаными вдоль какой-нибудь линии, могут быть совмещены с плоскостью (как, например, поверхность цилиндра или конуса). Однако многие поверхности, например шаровая, не могут быть совмещены с плоскостью, в связи с этим построение развертки может выполняться только приближенно.

Пусть требуется построить сечение поверхности конуса, стоящего на горизонтальной плоскости, плоскостью Р , которая параллельна плоскости V .

На рисунке 103 показана фронтальная плоскость Р , параллельная оси конуса и пересекающая его поверхность по гиперболе. Данная кривая проецируется на плоскость V без искажения.

Выполняя построение проекций сечения, вначале нужно найти секции характерных точек. В данном случае эти характерные точки представляют собой самые нижние и самые верхние ее точки.

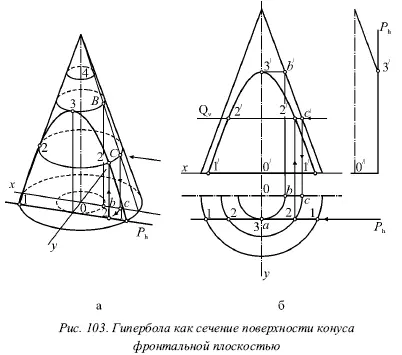
Нижние точки сечения.На рисунке 103а показаны две самые нижние точки сечения, они лежат в горизонтальной плоскости проекций и отмечены цифрой 1. Эти точки лежат на пересечении окружности основания с горизонтальным следом секущей плоскости P h. На эпюре рисунке 103б изображены их горизонтальные проекции 1, а их фронтальные проекции 1́ лежат на оси х .

Верхняя точка сечения (вершина гиперболы). На этом же рисунке дана профильная проекция 3˝ вершины гиперболы, которая непосредственно видна на профильной проекции конуса как пересечение его контура со следом Pw .

Следует отметить, что если профильная проекция конуса отсутствует, то, чтобы найти проекции вершины гиперболы (линии сечения), нужны некоторые вспомогательные построения. При этом любая горизонтальная плоскость Q пересекает конус по окружности, которая проецируется на горизонтальную плоскость Н без искажения. Эта окружность проектируется на фронтальную плоскость проекций в виде отрезка, который равен ее диаметру и который заключен между контурными образующими конуса. Если провести горизонтальную плоскость Q достаточно близко к основанию конуса, то часть данной окружности будет отсечена плоскостью Р (окружностью 2–2). Если провести такую плоскость несколько ближе к вершине, тогда окружность целиком сохранится (окружность 4). Требуется найти такое положение горизонтальной плоскости, которое даст самую большую целую окружность (окружность 3). Эта плоскость будет касаться гиперболы в вершине, она же определит положение искомой точки 3́.