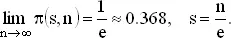Покажем, что вероятность в правой части (1) убывает, когда i возрастает, а вероятность в левой части (1) возрастает с возрастанием i , и потому существует выбор шага i , после которого предпочтительнее удержать максимальное приданое, нежели продолжать испытания. Вычисляя затем вероятность выигрыша для такой стратегии, найдем оптимальный выбор значения s .
После нескольких первых ходов в этой игре мы можем еще прибегнуть ко всем стратегиям, определяемым последующими вытаскиваниями, так как мы всегда можем пропустить часть билетов, пока не достигнем нужного нам числа билетов. Следовательно, вероятность в правой части неравенства (1) не возрастает с ростом i . При i = 0 это искомая оптимальная вероятность, а при i = n − 1 эта вероятность равна 1/ n как вероятность выигрыша при выборе на последнем шагу.
Вероятность того, что на i -м шагу максимальное приданое больше всех имеющихся, равна вероятности того, что наилучший номер находится на одном из первых i билетов, а именно, равна i / n , что является строго возрастающей от 1/ n до 1 функцией от i . Поэтому значение i / n в какой-то точке превосходит вероятность выигрыша при продолжении испытаний. Таким образом, оптимальная стратегия может быть задана следующим правилом: пропустить s − 1 первых номеров и выбрать затем первого лидера, т. е. первый номер, который больше всех предыдущих. Сосчитаем вероятность выигрыша для такой стратегии. Вероятность правильного решения есть вероятность появления ровно одного лидера между s -м шагом и n -м. Вероятность того, что наилучший билет появился на k -м шагу, равна 1/ n . Вероятность того, что максимум первых k − 1 номеров появился среди первых s − 1 номеров, есть ( s − 1)/( k − 1). Произведение ( s − 1)/[ n ·( k − 1)] дает вероятность того, что мы выиграем при выборе k , s ≤ k ≤ n . Суммируя эти числа, получим вероятность π( s , n ) получения наилучшего приданого при оптимальной стратегии
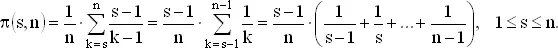 (2)
(2)
Так как первое вытаскивание всегда дает максимальный номер, то π(1, n) = 1/ n . Заметим, что при n = 4, s = 2 имеем π(1, n ) = 11/24, как и в нашем примере.
Оптимальное значение s , скажем, s *, есть минимальное s , для которого имеет место неравенство (1), т. е. это наименьшее s , для которого
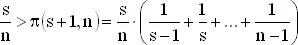 (3)
(3)
или, что равносильно, такое s , для которого
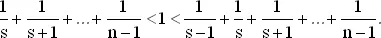 (4)
(4)
Оптимальное значение s и вероятности выигрыша для задачи о приданных
| n |
s |
π( s , n ) |
n |
s |
π( s , n ) |
| 1 |
1 |
1.000 |
10 |
4 |
0.399 |
| 2 |
1 |
0.500 |
20 |
8 |
0.384 |
| 3 |
2 |
0.500 |
50 |
19 |
0.374 |
| 4 |
2 |
0.458 |
100 |
38 |
0.371 |
| 5 |
3 |
0.433 |
∞ |
n / e |
1/ e ≈ 0.368 |
Эта таблица дает оптимальные значения s и соответствующие им вероятности правильного решения для небольших значений n . Для n = 100 следует пропустить 37 приданных и выбрать после этого первое максимальное.
Большие значения n
Для больших значений n мы можем аппроксимировать сумму 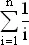 выражением ln( n ) + C , где С — постоянная Эйлера. Используя это приближение в формуле (2) для больших s и n , получаем
выражением ln( n ) + C , где С — постоянная Эйлера. Используя это приближение в формуле (2) для больших s и n , получаем
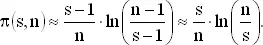 (5)
(5)
Аналогично приближения для правой и левой частей неравенства (4) показывают, что ln( n / s ) ≈ 1, и, значит, s ≈ n / e . Подставляя эти результаты в (5), находим
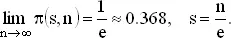
Подводя итог, видим, что для больших значений n оптимальная стратегия пропускает приблизительно 1/ e часть билетов и останавливается после этого на первом максимальном приданом, причем вероятность правильного решения равна приближенно 1/ e .
Читать дальше

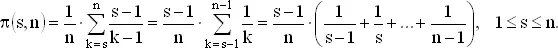 (2)
(2)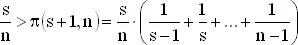 (3)
(3)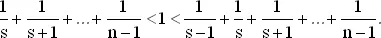 (4)
(4)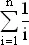 выражением ln( n ) + C , где С — постоянная Эйлера. Используя это приближение в формуле (2) для больших s и n , получаем
выражением ln( n ) + C , где С — постоянная Эйлера. Используя это приближение в формуле (2) для больших s и n , получаем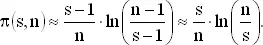 (5)
(5)