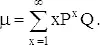Для того чтобы уравнение имело вещественные корни, необходимо и достаточно, чтобы
b ² − c ≥ 0.
На приведенном рисунке изображена парабола b ² = c и показана область, где наше уравнение имеет вещественные корни для B = 4.
Нетрудно подсчитать, что площадь незаштрихованной области равна 4/3∙ B 3/2(при B ≥ 1), а площадь всего квадрата, конечно, равна 4 B ². Следовательно, вероятность того, что корни комплексные, равна 1/3∙√ B . При B = 4 ответ равен 1/6. С ростом B 1/√ B стремится к нулю, так что вероятность того, что корни вещественные, стремится к 1.
Следует заметить, что эта задача отличается от такой же задачи, связанной с уравнением ax ² + 2 bx + c = 0. Конечно, можно разделить на a , но если a , b и c были независимы и равномерно распределены в некотором кубе, то b / a и c / a уже зависимы и распределены неравномерно.
51. Решение вадачи о двумерном случайном блуждании
В одномерном случайном блуждании (см. задачу 35 «На краю утеса», последняя часть решения) мы нашли, что вероятность возвращения частицы в начало есть l, если вероятности шагов налево и направо одинаковы. Но положение дел все же весьма деликатно сбалансировано. Если бы одна из вероятностей отличалась от 1/2, то частица удалилась бы в бесконечность. В случае двух измерений можно предположить, что у частицы больше возможностей для ухода в бесконечность. Выясним, так ли это. Мы постараемся найти среднее число возвращений частицы в начало и отсюда определить значение вероятности возвращения частицы. Прежде всего, сколько раз частица вернется в начало? Если P есть вероятность возвращения, то 1 − P = Q есть вероятность того, что возвращения не будет. Тогда вероятность ровно x возвращений есть P xQ , так как после каждого возвращения частицу можно рассматривать как снова выходящую из начала. Если бы P было известно, то среднее число возвращений в начало координат можно было бы найти, суммируя геометрический ряд вида
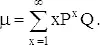
Из задачи 4 об испытаниях до первого успеха видно, что среднее число возвращений есть величина, обратная к вероятности успеха. В упомянутой задаче успех заканчивал серию испытаний, в нашей же задаче серию заканчивает невозвращение в начало, так что среднее число испытаний до первого успеха равно 1/ Q . Следовательно, среднее число успехов равно 1/ Q − 1. Если Q = l, то среднее число успехов равняется 0, и с вероятностью 1 частица будет потеряна и никогда не вернется. С другой стороны, чем меньше Q , тем больше среднее число возвращений. Действительно, каждому значению Q отвечает среднее число возвращений и для каждого среднего числа найдется соответствующее Q . Если среднее число возвращений перед окончательным уходом бесконечно (неограниченно), то Q должно быть равным нулю, а P равным 1. Более формально, P → 1 при µ → ∞. Теперь видно, что для решения задачи о двумерном блуждании мы должны подсчитать значение µ.
Выходя из начала, частица может попасть в него обратно лишь после четного числа шагов. Более того, ее путь может быть представлен как «произведение» двух независимых одномерных случайных блужданий, каждое из которых начинается в начале координат, и одно происходит в вертикальном направлении, а другое — в горизонтальном направлении. После двух шагов горизонтальная компонента x имеет распределение
| x |
-2 |
0 |
2 |
| P ( x ) |
1/4 |
2/4 |
1/4 |
Вертикальная компонента после двух шагов распределена точно так же, и вероятности их совместного распределения в девяти точках выглядят следующим образом:
|
|
Распределение X |
|
|
x |
-2 |
0 |
2 |
|
|
P ( x ) |
1/4 |
2/4 |
1/4 |
| Распределение Y |
|
|
|
| y |
P ( y ) |
|
P ( x , y ) |
| 2 |
1/4 |
|
1/16 |
2/16 |
1/16 |
| 0 |
2/4 |
|
2/16 |
4/16 |
2/16 |
| -2 |
1/4 |
|
1/16 |
2/16 |
1/16 |
| Совместное распределение X и Y после двух шагов |
Основной факт, на который мы хотим обратить внимание, состоит в том, что вероятность возвращения в начало есть 4/16, и это число ввиду независимости компонент блуждания есть произведение P ( X = 0) на P ( Y = 0). Это допускает следующую интерпретацию. После двух шагов 25 % частиц в среднем вернется в начало. Вклад в среднее число возвращений в начало координат будет тогда равен 4/16·1 + 12/16·0 = 4/16. Вычислим вероятность того, что частица попадет в начало после 2, 4, 6, ... шагов, и, сложив все эти значения, найдем математическое ожидание числа возвращений частицы в начало.
Читать дальше