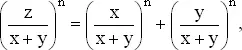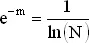Итак, оценкой числа π в этом случае является 4∙5.2/(62/10) ≈ 3.35 вместо 3.14. При другом опыте, состоящем также из 10 подбрасываний, было получено 67 пересечений, что дает оценку 3.10.
56. Обсуждение задачи о двух урнах
Е. Молина предложил эту задачу, чтобы дать формулировку знаменитой проблемы Ферма на вероятностном языке.
Пусть z обозначает число белых шаров в первой урне, x — число белых шаров и y — число черных шаров во второй урне. Тогда задача состоит в том, чтобы найти целые числа n , x , y и z такие, что
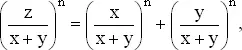
или
z n = x n + y n .
Хотя для многих значений n известно, что это уравнение не имеет корней, но не установлено, так ли это при всех n ≥ 3. Доказано, однако, что целочисленных решений нет при n < 2000.
57. Обсуждение задачи о простых делителях
Из таблиц или из непосредственного расчета нетрудно выписать распределения числа простых делителей для небольших значений N .
В таблице 1 приведены результаты для N = 100 и N = 1000 вместе со средними x̅ и дисперсиями s ².
Таблица 1. Распределение числа простых делителей с учетом их кратностей для N = 100 и N = 1000 вместе со средними x̅ и дисперсиями s² (x = число простых делителей)
| N = 100 |
|
N = 1000 |
| x |
f |
fx |
fx ² |
x |
f |
| 1 |
26 |
26 |
26 |
1 |
169 |
| 2 |
34 |
68 |
136 |
2 |
299 |
| 3 |
22 |
66 |
198 |
3 |
247 |
| 4 |
12 |
48 |
192 |
4 |
149 |
| 5 |
4 |
20 |
100 |
5 |
76 |
| 6 |
2 |
12 |
72 |
6 |
37 |
|
100 |
240 |
724 |
7 |
14 |
| x̅ = 2.40, s ² = ∑ f ∙( x − x̅ )2/ N = ∑ f ∙ x ²/ N − x̅ ² = 1.48. |
8 |
7 |
| 9 |
2 |
|
1000 |
| x̅ = 2.88, s ² = 2.22 |
Из этой таблицы, например, видно, что среди первых 100 натуральных чисел ровно 26 простых, у 34 чисел два простых делителя и только у двух шесть простых делителей.
Распределение числа делителей при N = 100 напоминает выборку из закона Пуассона. Для пуассоновских распределений среднее равно дисперсии. Из таблицы видно, что для N = 100 среднее несколько больше дисперсии. Если рассмотреть величину x − 1 вместо x , то новое среднее будет равно 1.40, а дисперсия, равная 1.48, не изменится. Полезно сравнить полученные результаты с табличными вероятностями для закона Пуассона. (Сумма элементов последней строки первой половины табл. 2 не равна 100 из-за округления значений.)
Таблица 2. Частоты простых делителей x и соответствующие величины для распределения Пуассона со средним m
| N = 100 |
| x − 1 |
0 |
1 |
2 |
3 |
4 |
≤ 5 |
| Наблюденные частоты |
26 |
34 |
22 |
12 |
4 |
2 |
| Пуассоновские частоты для m = 1.4 |
24.7 |
34.5 |
24.2 |
11.3 |
3.9 |
|
| N = 1000 |
| x − 1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
≤ 8 |
| Наблюденные частоты |
169 |
299 |
247 |
149 |
76 |
37 |
14 |
7 |
2 |
| Пуассоновские частоты для m = 1.9 |
150 |
284 |
270 |
171 |
81 |
31 |
10 |
3 |
1 |
| Пуассоновские частоты для m = 1.8 |
165 |
298 |
268 |
161 |
72 |
26 |
8 |
2 |
1 |
Видно, что при N = 100 совпадение лучше, нежели при N = 1000. Для N = 1000 более точная аппроксимация при небольших значениях x − 1 может быть получена за счет выбора меньшего математического ожидания пуассоновского распределения.
Таблица 2 подтверждает предположение о пуассоновости распределения числа простых делителей, однако картина слишком сложна, чтобы можно было угадать вид параметра этого закона для больших N .
Мы знаем, что вероятность отсутствия простых делителей, т. е. того, что само число просто, равна приближенно 1/ln( N ). Для закона Пуассона вероятность появления 0 равна e −m , где m — математическое ожидание этого распределения (см. задачу 29). Отсюда выводим:
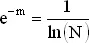
и
− m = −ln(ln( N )),
или
m = ln(ln( N )).
Любопытно сравнить эту формулу с полученными ранее результатами.
Имеем
ln(ln(100)) = 1.53,
что надо сравнить со средним 1.4 при N = 100. Для N = 1000 среднее равнялось 1.88, а
Читать дальше