Представляется замечательным, что в этой игре, которая на первый взгляд дает вероятность 1/ n выигрыша, существует простая стратегия с вероятностью правильного решения больше чем 1/3 даже для больших значений n .
48. Решение задачи о выборе наибольшего случайного числа
Довольно понятно, что надо выбрать первое же число, если оно достаточно велико, например, равно 0.999, потому что вероятность получить не меньшее же число позднее, равна только
1 − (0.999)99 ≈ 0.1.
Как и в предыдущей задаче, мы должны выбирать между очередным максимальным появившимся номером и шансом на то, что одно из последующих чисел будет больше этого номера, причем мы его выберем. Рассмотрим процедуру решения с конца. Если мы не сделали выбор до последнего шага, то останавливаемся на последнем числе и выигрываем или проигрываем. Если выбор не произведен до предпоследнего вытягивания, и появилось максимальное число (самое большое до сих пор), мы выбираем его, если оно больше 1/2, отказываемся от него, если оно меньше 1/2, и поступаем произвольным образом в случае 1/2. Если это число меньше 1/2, то шанс на выигрыш больше при продолжении испытаний.
Если третье с конца число x максимально, то вероятности появления 0, 1 или 2 больших чисел после этого равны x ², 2 x ∙(1 − x ) и (1 − x )² соответственно. Если мы пропустим x и выберем следующее большее, чем x , число, то вероятность выигрыша окажется равной
2 x ∙(1 − x ) + 1/2∙(1 − x )²,
так как если дальше будет 0 больших чисел, мы не выиграем, если 1, то выиграем наверняка, и если два числа, больших x , то мы выберем наибольшее с вероятностью 1/2. Если мы пропускаем какое-то число при определенном вытаскивании, то при последующих вытягиваниях это положение может измениться, так как нам, возможно, придется остановиться на этом числе, ввиду уменьшения шансов на появление большего. Следовательно, если имеются два числа, больших «порогового» уровня x в нашей последовательности, то мы заведомо выберем первое. Оно лишь с вероятностью 1/2 наибольшее из этих двух чисел. Таким образом, если на некотором шагу мы отказались от «порогового» числа, то можно быть уверенным в том, что оптимальная стратегия выбирает первое число, значение которого превосходит данный «пороговый» уровень.
Определим это «пороговое» значение x для третьего с конца шага. Это число удовлетворяет уравнению
x² = 2 x ∙(1 − x ) + 1/2∙(1 − x )².
Здесь x ² есть вероятность того, что мы выиграем, остановившись на числе x , а правая часть есть вероятность выиграть, если мы отказались от x . «Пороговый» уровень, как нетрудно проверить, равен
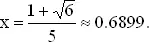
Таким образом, мы выбираем максимальное число третье с конца, если его значение превосходит 0.6899.
Вообще, если остается r билетов и появилось максимальное число, то мы выберем его, если оно превосходит «пороговое» значение x , вычисляемое из уравнения
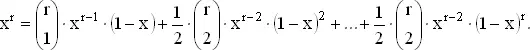 (1)
(1)
Для нахождения x при небольших значениях r это уравнение можно решать численно, используя, например, таблицы вероятностей биномиального закона. В нижеследующей таблице «пороговых» уровней приведены некоторые из них.
Чтобы найти приближенное решение, заметим, что 1 − x уменьшается по мере возрастания r , и главный вклад в правую часть уравнения (1) дается первым членом. Таким образом,
x r ≈ r ∙x r − 1∙(1 − x ), или x ≈ r /( r + 1).
С другой стороны, деля обе части уравнения (1) на x r и полагая z = (1 − x )/ x , получаем
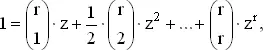 (2)
(2)
откуда определяется z .
Наконец, так как приближенно z = 1/ r , положим
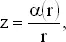
где α( r ) — функция, близкая к постоянной. Так,
α(1) = 1
α(2) = 0.8990,
α(3) = 0.8668,
α(4) = 0.8509,
α(5) = 0.8415.
Полагая в (2) z = α( r )/ r и устремляя r к бесконечности, получаем
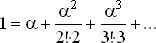 (3)
(3)
Здесь α — предельное значение α( r ), α = 0.8043.Хотя существуют и лучшие приближения для α( r ), заменим α( r ) на α. Тогда
Читать дальше

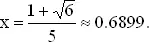
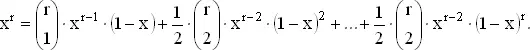 (1)
(1)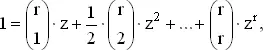 (2)
(2)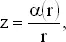
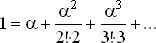 (3)
(3)










