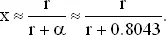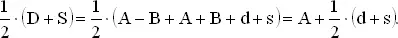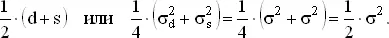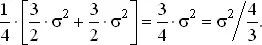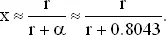
Эта формула для x дает результаты, приведенные в последнем столбце таблицы.
Таблица «пороговых» уровней и их приближений
| Число оставшихся испытаний |
Решение уравнения (1) |
r /( r + a ) |
Число оставшихся испытаний |
Решение уравнения (1) |
r /( r + a ) |
| 1 |
0.5000 |
0.5542 |
9 |
0.9160 |
0.9180 |
| 2 |
0.6899 |
0.7132 |
10 |
0.9240 |
0.9256 |
| 3 |
0.7758 |
0.7886 |
11 |
0.9305 |
0.9319 |
| 4 |
0.8246 |
0.8326 |
12 |
0.9361 |
0.9372 |
| 5 |
0.9856 |
0.8614 |
13 |
0.9408 |
0.9417 |
| 6 |
0.8778 |
0.8818 |
14 |
0.9448 |
0.9457 |
| 7 |
0.8939 |
0.8969 |
15 |
0.9484 |
0.9491 |
| 8 |
0.9063 |
0.9086 |
|
|
|
Поскольку в данной игре больше информации, чем в игре из предыдущей задачи, то шансы на выигрыш также больше. Если число билетов равно 2, то игроку следует выбрать первое число, если оно больше 1/2, а в противном случае избрать второе. Вероятность правильного решения в этом случае равна 3/4. Увеличение числа билетов от 1 до 2 значительно уменьшило вероятность выигрыша. Некоторые геометрические соображения, которые мы не будем здесь приводить, показывают, что для n = 3 вероятность правильного выбора равна приблизительно 0.684. Для больших n эта вероятность равняется приближенно 0.580.
49. Решение задачи об удвоении точности
Да. Пусть A — длина длинного стержня, а B — длина короткого. Можно положить эти стержни рядом и измерить разность длин A − B , а затем приложить их один к другому и измерить сумму длин A + B . Пусть D и S обозначают наблюденные длины A − B и A + B соответственно. Тогда оценка для A есть 1/2( S + D ) и оценка для B есть 1/2( S − D ). Далее, D = A − B + d , S = A + B + s , где d и s — случайные ошибки. Следовательно,
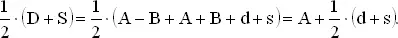
В среднем ошибка 1/2( d + s ) будет нулевой, поскольку d и s имеют средние нуль. Дисперсия оценки A есть дисперсия
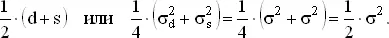
Это значение совпадает со значением для дисперсии среднего двух независимых наблюдении. Таким образом, оба наблюдения внесли полный вклад в измерение A . Точно так же дисперсия оценки B равняется σ²/4. Следовательно, делая два измерения — одно для разности, другое для суммы — мы получаем оценки, точность которых равна точности при четырех рениях, по два на каждый стержень в отдельности.
Для получения столь хороших результатов мы должны как можно точнее соединить концы стержней. Если этого сделать нельзя, то можно считать, что в результаты измерений входит ошибка, связанная с неидеальным совпадением концов стержня. Если эта случайная ошибка имеет штандарт σ√2, то одному измерению суммы или разности отвечает штандарт σ√3/√2, и дисперсия нашей оценки A будет равна
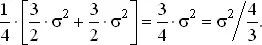
При этих предположениях наша точность будет точно такой же, как и точность при 4/3 независимых измерениях вместо 2, но все же больше точности одного прямого измерения.
Мы можем обосновать предположение о том, что ошибка от неточного совпадения концов имеет штандарт σ/√2, следующим образом. Представим себе s (или d ) как сумму двух независимых ошибок измерения, каждую с дисперсией σ²/2. Тогда сумма слагаемых ошибок имеет дисперсию, которую мы считали
равной σ². Если мы припишем дисперсию σ²/2 и третьему слагаемому, то такая модель будет согласовываться с исходной.
50. Решение задачи о квадратных уравнениях со случайными коэффициентами
Для того чтобы вопрос задачи имел смысл, предположим, что точка ( b , c ) равномерно распределена на квадрате с центром в начале координат и стороной 2 B (рис. 22). Решим задачу при фиксированном B , а затем устремим B к бесконечности, так что b и c могут принимать любые значения.
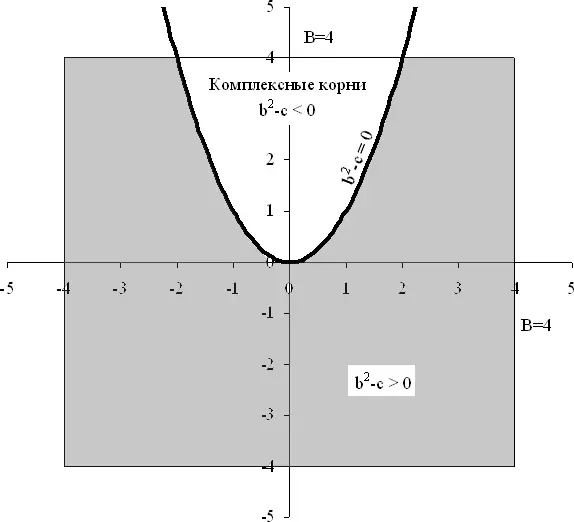
Рис. 22. Серая область отвечает случаю вещественных корней.
Читать дальше