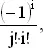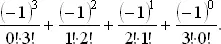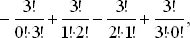Распределение числа совпадений, n = 3
| Число совпадений |
0 |
1 |
2 |
3 |
| Вероятность |
2/6 |
3/6 |
0/6 |
1/6 |
Приведем также соответствующую таблицу для n = 4. Легко заметить, что вероятность того, что произойдет n совпадений, равна 1/ n !, поскольку только одной из n ! перестановок отвечает n совпадений.
| Число совпадений |
0 |
1 |
2 |
3 |
4 |
| n = 1, вероятность |
0 |
1 |
|
|
|
| n = 2, вероятность |
1/2 |
0 |
1/2 |
|
|
| n = 3, вероятность |
2/6 |
3/6 |
0 |
1/6 |
|
| n = 4, вероятность |
9/24 |
8/24 |
6/24 |
0 |
1/24 |
Отметим, что математическое ожидание каждого распределения равно 1, как указано в предыдущей задаче.
Пусть P ( r / n ) обозначает вероятность ровно r совпадений при распределении n объектов. Эти r совпадений могут быть получены за счет совпадения r фиксированных объектов и несовпадения остальных. Так, например, вероятность того, что совпадают именно r первых объектов, равна
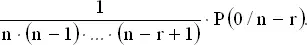
Число различных выборов r объектов из n равно 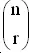 так что
так что
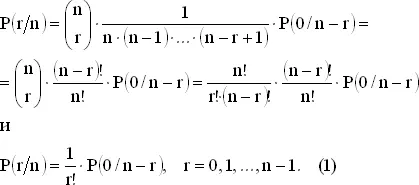
При r = n , как мы знаем, P ( n / n ) = 1/ n !, и мы можем положить P (0/0) = 1.
Проверим справедливость соотношения (1) при n = 4, г = 2. Согласно (1)
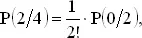
а из нашей таблицы видно, что
P (2/4) = 6/24,
P (0/2) = 1/2
и 6/24 = 1/4, что подтверждает (1) в этом частном случае.
Мы знаем также, что сумма вероятностей по всем возможным числам совпадений при заданном значении n равна 1, т. е.
P (0/ n ) + P (1/ n ) + ... + P ( n − 1/ n ) + P ( n / n ) = 1.
Используя (1), запишем это соотношение как
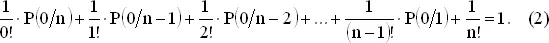
Так как P ( n / n ) = 1/ n !, то отсюда можно последовательно находить значения P (0/ n ).
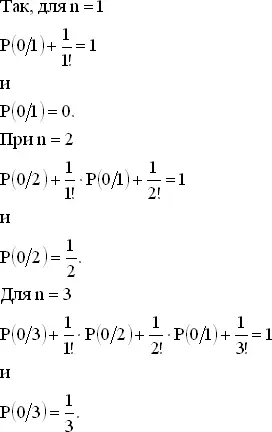
Итак, мы можем найти в принципе значение P (0/ n ) при любом n , но не располагаем общей формулой для вычисления P (0/ n ). Как и в некоторых других задачах, здесь помогает вычисление последовательных разностей. Подсчитаем P (0/ n ) − P (0/ n − 1) для различных значений n . Имеем
P (0/1) − P (0/0) = 0 − 1 = −1 = −1/1!,
P (0/2) − P (0/1) = 1/2 − 0 = 1/2 = 1/2!,
P (0/3) − P (0/2) = 2/6 − 1/2 = −1/6 = −1/3!,
P (0/4) − P (0/3) = 9/24 − 2/6 = 1/24 = 1/4!.
Эти выкладки наводят на мысль о том, что искомые разности имеют вид (-l) r / r !, т. е.
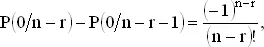
Суммируя эти разности, получаем
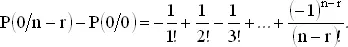
Записывая P (0/0) в виде 1/0!, получаем
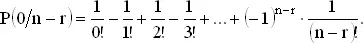 (3)
(3)
Осталось проверить теперь справедливость нашей догадки. Нам надо вычислить
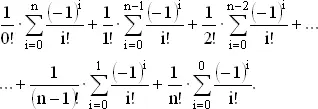 (4)
(4)
Не следует терять хладнокровия. при виде этого зловещего выражения. Ведь сумма в (4) образована слагаемыми вида
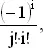
где индекс j отвечает множителю, стоящему перед знаком суммы, а индекс i соответствует отдельным членам этой суммы. Переставим местами слагаемые так, чтобы сумма i + j была постоянной. Так, для i + j = 3 получим
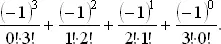
Умножая на 3!, получаем более знакомое выражение
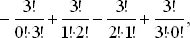
которое с помощью биномиальных коэффициентов может быть записано в виде
Читать дальше

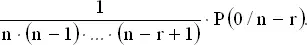
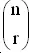 так что
так что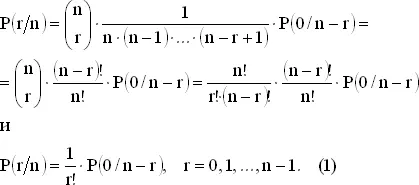
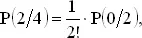
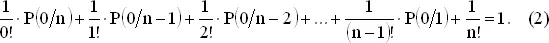
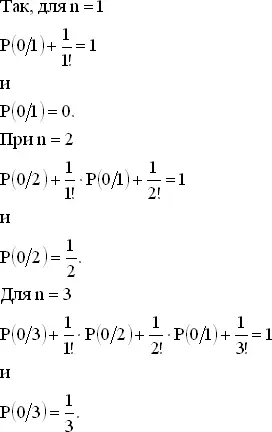
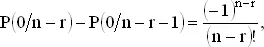
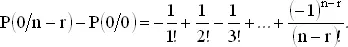
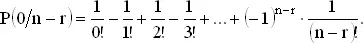 (3)
(3)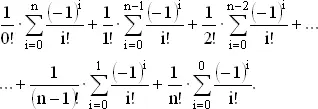 (4)
(4)