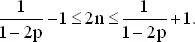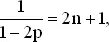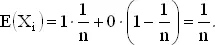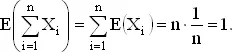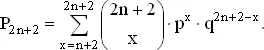
Игра, составленная из 2 n + 2 партий, может быть рассмотрена как игра из 2 n туров с добавлением еще двух туров. Если только игрок A не набрал n или n + 1 очко в игре из 2 n туров, то он остается выигравшим или проигравшим в игре из 2 n + 2 партий в зависимости от того, выиграл он или проиграл в игре из 2 n партий.
Итак, вычислим (1) вероятность получения n + 1 очка в первых 2 n партиях и проигрыша в следующих двух, равную
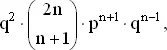
и (2) вероятность получения n очков в первых 2 n партиях и выигрыша в следующих двух, которая равняется
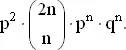
Если N = 2 n — оптимальный выбор для A , то P N − 2≤ P N , P N ≥ P N + 2. Из предыдущих рассуждений следует, что эти неравенства эквивалентны следующим:
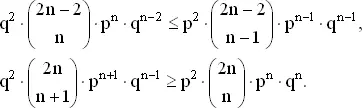 (1)
(1)
После незначительных преобразований (при которых исключается тривиальный случай p = 0) неравенства (1) сводятся к следующим:
( n − 1)· q ≤ np , nq ≥ ( n + 1)· p . (2)
Отсюда выводим
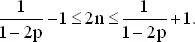
Итак, если только 1/(1 − 2 p ) не является нечетным числом, то значение N определяется единственным образом, как ближайшее четное число, меньшее 1/(1 − 2 p ). Если же 1/(1 − 2 p ) нечетное число, то для обоих четных чисел 1/(1 − 2 p ) − 1 и 1/(1 − 2 p ) + 1 оптимальные вероятности одни и те же, т. е. если
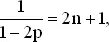
то
P 2 n = P 2 n + 2.
Для p = 0.45 в качестве оптимального числа партий получаем 1/(1 − 0.9) = 10.
45. Решение задачи о среднем числе совпадений
Рассмотрим сначала задачу с колодой карт. Если в колоде 52 карты, то каждая карта с вероятностью 1/52 занимает место, уже занятое такой же картой. Так как общее число возможных мест для каждой карты равно 52, то среднее число совпадений равно 52·1/52 = 1. Таким образом, в среднем происходит только одно совпадение. Если бы колода состояла из n различных карт, то среднее число совпадений прежнему равнялось бы 1, так как n ·(1/ n ) = 1. Этот вывод основывается на теореме о том, что среднее суммы есть сумма средних.
Более формально, с каждой парой карт может быть связана случайная величина X i , которая равна 1 в случае, если карты одинаковы, и 0, если карты различны. Имеем
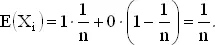
Наконец, общее число совпадений равно ∑ X i и в силу уже упоминавшейся теоремы
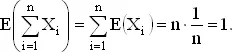
46. Решение задачи о вероятностях совпадений
Эта задача родственна задаче 28, в которой мы впервые встретились с законом Пуассона. Однако в задаче о фальшивомонетчике в силу независимости испытаний появление фальшивой монеты было равновероятно на каждом шагу, в настоящей же задаче совпадения для каждой пары не являются независимыми. Например, если n − 1 пар совпали, то необходимо совпадет и n -я пара, так что эти события действительно зависимы. Тем не менее при больших значениях n степень зависимости невелика, так что, казалось бы, вероятность r совпадений в этой задаче должна быть близка к вероятности обнаружения фальшивых монет, задаваемой распределением Пуассона. В конце мы сравним решение такой задачи с ответом, получаемым из закона Пуассона со средним 1.
При решении таких задач оказывается полезным рассмотрение частных случаев, отвечающих небольшим значениям n . При n = 1 совпадение неизбежно. При n = 2 вероятность отсутствия совпадения равна 1/2, вероятность двух совпадений также равняется 1/2. При n = 3 занумеруем карты цифрами 1, 2 и 3 и запишем в таблицу 6 возможных перестановок для верхней колоды при фиксированном порядке (1, 2 ,3) нижней.
Перестановки и совпадения, n = 3
| Нижняя колода |
1 |
2 |
3 |
Число совпадений |
| Перестановки верхней колоды |
1 |
2 |
3 |
3 |
| 1 |
3 |
2 |
1 |
| 2 |
1 |
3 |
1 |
| 2 |
3 |
1 |
0 |
| 3 |
1 |
2 |
0 |
| 3 |
2 |
1 |
1 |
Отсюда получаем
Читать дальше

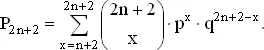
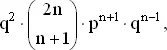
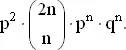
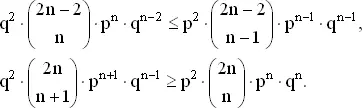 (1)
(1)