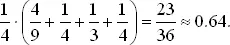
Если вытягивать оба шара без возвращения, то вероятность угадать приблизительно равна 5/8, а при возвращении 21.5/36 (0.625 < 0.597).
22. Решение задачи о выборах
При a = 3 и b = 2 всеми возможными равновероятными последовательностями извлечения бюллетеней являются следующие:
АААВВ *ААВВА *АВВАА
*АВАВА *ВАВАА *ВААВА
*ВВААА ААВАВ *АВААВ
*ВАААВ ,
где звездочкой отмечены комбинации, в которых имеет место равновесное положение. Таким образом, в нашем случае искомая вероятность равна 8/10.
Перейдем теперь к общей ситуации произвольных a и b . Рассмотрим сначала те последовательности, в которых первое равновесное положение достигается в случае, когда подсчитаны 2 n бюллетеней, n ≤ b . Каждой последовательности, в которой A лидирует до первого ничейного результата, соответствует единственная последовательность, в которой лидирует B . Так, при n = 4 последовательности
ААВАВАВВ
с лидером A отвечает последовательность
ВВАВАВАА
в которой лидирует B . Эта последовательность получается из первой заменой A на B и B на A .
Итак, число последовательностей, в которых A лидирует до первой ничьей, равно числу последовательностей с лидером B . Задача сводится, таким образом, к вычислению вероятности равновесного положения, до которого лидирует B .
Так как за A подано большее количество голосов, то рано или поздно A становится лидером. Если первый бюллетень подан за B , то ничья неизбежна. Единственной возможностью ничьей с B , лидирующим в начале, является случай, когда первый бюллетень подан за B . Вероятность того, что это так, равна b /( a + b ). Но это же значение равно вероятности ничьей с лидирующим в начале A , и, таким образом, вероятность ничейного положения равна
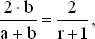
где r = a / b . Заметим, что если a много больше, чем b , т. е. когда r велико, вероятность ничьей мала (что интуитивно вполне понятно). Формула верна также и при b = a , так как в этом случае вероятность ничьей равна единице.
23. Решение задачи о ничьих при бросании монеты
Ниже мы обобщим метод решения задачи 22 и покажем, что вероятность отсутствия ничейного результата (при N четном и N нечетном) равна
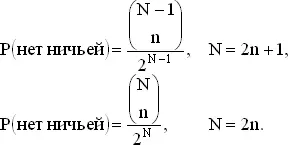
Эти формулы показывают, что указанная вероятность одна и та же для четного N и для следующего за ним нечетного числа N + 1. Например, когда N = 4, надо применить вторую формулу. Шестнадцатью возможными исходами являются
ААAA BAAA ABBA BABB
*AAAB AABB BABA *BBAB
*AABA ABAB BBAA *BBBA
ABAA BAAB ABBB *BBBB
где звездочкой отмечены комбинации с равновесным положением.
Поскольку число сочетаний из 4 по 2 равно 6, то вторая формула действительно верна для этого значения N .
При N = 2 n вероятность x выигрышей A есть 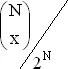 . Если x ≤ n , то вероятность ничьей есть 2 x / N (на основании задачи 22), а при x ≥ n эта вероятность равна 2·( N − x )/ N . Чтобы получить вероятность ничьей, находим вероятность x выигрышей, умножим ее на условную вероятность ничьей при x выигрышах и просуммируем полученные выражения, что дает
. Если x ≤ n , то вероятность ничьей есть 2 x / N (на основании задачи 22), а при x ≥ n эта вероятность равна 2·( N − x )/ N . Чтобы получить вероятность ничьей, находим вероятность x выигрышей, умножим ее на условную вероятность ничьей при x выигрышах и просуммируем полученные выражения, что дает
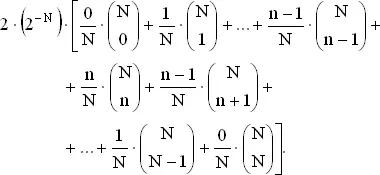 (1)
(1)
Если подставить в это выражение формулу для биномиальных коэффициентов и произвести необходимые сокращения, то с точностью до слагаемого
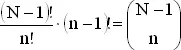
получим 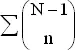 , где суммирование ведется по всем возможным значениям x . Следовательно, мы можем переписать выражение (1) в виде
, где суммирование ведется по всем возможным значениям x . Следовательно, мы можем переписать выражение (1) в виде
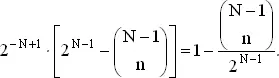 (2)
(2)
Читать дальше

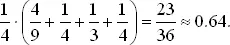
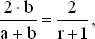
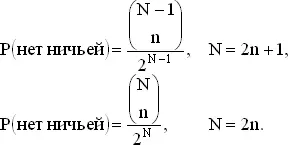
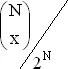 . Если x ≤ n , то вероятность ничьей есть 2 x / N (на основании задачи 22), а при x ≥ n эта вероятность равна 2·( N − x )/ N . Чтобы получить вероятность ничьей, находим вероятность x выигрышей, умножим ее на условную вероятность ничьей при x выигрышах и просуммируем полученные выражения, что дает
. Если x ≤ n , то вероятность ничьей есть 2 x / N (на основании задачи 22), а при x ≥ n эта вероятность равна 2·( N − x )/ N . Чтобы получить вероятность ничьей, находим вероятность x выигрышей, умножим ее на условную вероятность ничьей при x выигрышах и просуммируем полученные выражения, что дает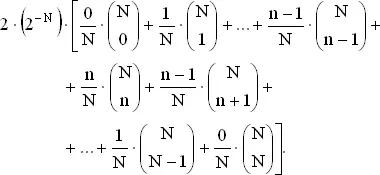 (1)
(1)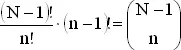
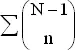 , где суммирование ведется по всем возможным значениям x . Следовательно, мы можем переписать выражение (1) в виде
, где суммирование ведется по всем возможным значениям x . Следовательно, мы можем переписать выражение (1) в виде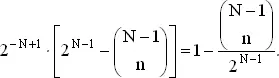 (2)
(2)










