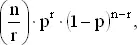
где p = m / n . Заменим p на m / n в этой формуле. Полученное выражение уже знакомо нам по задаче 28. Пусть n → ∞. Тогда мы снова приходим к распределению Пуассона
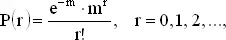
При m = 3 и r = 3 получаем значение 0.224.
То, что m действительно является средним этого распределения, проверяется непосредственно:
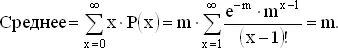
Чтобы получить численные результаты для больших значений m , где r = m , можно использовать таблицы [10] См., иапример, Л. Н. Большев, Н. В. Смирнов, Таблицы математической статистики «Наука», 1965, стр. 360 (прим. перев.) .
или формулу Стирлинга. Последняя дает
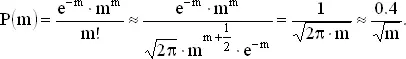
Численные примеры:
| m |
P ( m ) |
0,4√ m |
| 4 |
0.1954 |
0.200 |
| 9 |
0.1318 |
0.133 |
| 16 |
0.0992 |
0.100 |
30. Решение задачи о расчете булочника
Почему мы пользуемся предположением о распределении Пуассона? Отчасти потому, что задача допускает тогда красивое решение, а отчасти потому, что распределение действительно может быть близким к пуассоновскому, так как булочник имеет много клиентов, каждый из которых довольно редко покупает кекс. Если читателя беспокоит колебание числа покупок, связанное с разными днями недели, то будем говорить лишь о вторниках в течение лета.
Большинство обычно считает, что искомая вероятность равна 1/2.
Вероятность продать ровно r кексов есть e −20·20 r / r !, как известно из задачи 28. Заменив 20 на m , мы лучше выясним структуру задачи. Сумма вероятностей закона Пуассона есть ∑ e − m · m r / r ! или
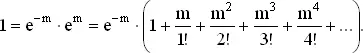 (A)
(A)
Нашей целью является выделение слагаемых, отвечающих нечетным количествам покупок. Известно, что
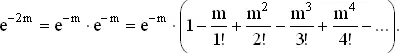 (B)
(B)
Сумма выражений (A) и (B) дает нам удвоенную вероятность четного числа кексов, так как члены с нечетными степенями m войдут в сумму с нулевыми коэффициентами, а члены с четными степенями — с коэффициентом 2. Следовательно, деля на 2, получим вероятность четного числа покупок (1 + e −2 m )/2. При m = 20 этот результат весьма близок к 0.5, так как число e −40мало́. С другой стороны, если булочник продает в среднем один специальный торт ко дню рождения за одну поездку, то вероятность того, что будет продано четное число таких тортов, равняется приблизительно 0.568.
31. Решение задачи о парных днях рождения
В задачах такого рода предполагается обычно, что 29 февраля не может быть днем рождения, и что всем остальным дням в году отвечает одинаковая вероятность.
Решим несколько более общую задачу. Пусть N обозначает число равновероятных дней, r — число людей. Вычислим вероятность того, что все эти люди родились в разные дни. Тем самым мы найдем и вероятность того, что хотя бы два человека родились в один и тот же день.
Для первого человека имеется N возможных дней, для второго — ( N − 1), не совпадающих с днем рождения первого, для третьего — ( N − 2), отличных от дней рождения первых двух и т. д., для r -го человека существует N − r + 1 возможностей. Общее число вариантов, при которых нет одинаковых дней рождения, равно
N ·( N − 1)·...·( N − r + 1) ( r сомножителей). (1)
Для определения интересующей нас вероятности надо найти еще общее число всевозможных расстановок дней рождения. Для каждого человека существует ровно N возможных дней, и общее число различных распределений дней рождения r людей равно
N r . (2)
Так как, согласно предположению, все дни равновероятны, то искомая вероятность равна отношению (1) и (2). Таким образом, вероятность того, что имеются по крайней мере два одинаковых дня рождения, равна
P r = 1 − N ·( N − 1)·...·( N − r + 1)/ N r . (3)
Точное вычисление значения (3) потребовало бы при больших значениях N таких, как 365, значительного числа выкладок, чего в нашем случае можно избежать за счет использования таблицы логарифмов, представляя искомую вероятность в виде N ! / ( N − 2)!· N r . Имеем
Читать дальше

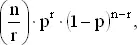
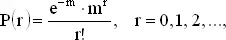
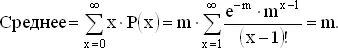
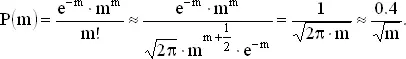
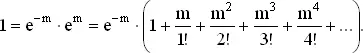 (A)
(A)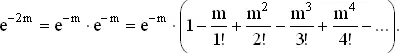 (B)
(B)










